Bevezetés A robotkutatásokkal kapcsolatban napjainkban számtalan új eredmény születik. A robotok, mint bizonyos korlátok között működő autonóm, vagy ember által kontrollált fél autonóm eszközök iránt egyre nagyobb az igény mind a katonai-, mind a civil szférában. Az autonóm helyváltoztatásra alkalmas robotok esetén a robottechnika egy szintén kiemelkedő fejlődést mutató számítógép alkalmazási területhez kapcsolódik. Ezt a szakterületet térinformatikának hívjuk. Cikkemben a robotkutatások és a térinformatika kapcsolódását kívánom bemutatni, kizárólag a Földön, vagy annak közvetlen közelében mozgó (közlekedő) eszközök vonatkozásában. Külön tématerületet képez mind a robotkutatásokban, valamint a térinformatikában, a Naprendszerünkben, vagy azon kívüli autonóm közlekedés és tájékozódás. A földi- és föld közeli légi közlekedés, tájékozódás és autonóm helyváltoztatás hatékony segítője a műholdas navigációs rendszer. A GPS-t (Global Position System) a térinformatika - mankójának - tekinthetjük. Jelenleg több tájékozódásra alkalmas műholdas helymeghatározó rendszer létezik, úgymint az amerikai NAVSTAR GPS, valamint az orosz GLONAS és készül az európai GALILEO... Civil alkalmazások leginkább az amerikai rendszerre épülnek. Az ok igen egyszerű, a kereskedelmi forgalomban immár tömegcikként kapható GPS vevők az amerikai GPS rendszer jeleinek vételére alkalmas.
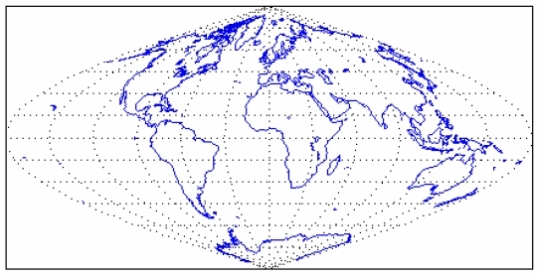
Térképek, dátumok, digitális tér Az életterünk, a Föld feltérképezése az emberiség régi vágya. Az emberiség először a lakhelye és annak környezetét próbálta felderíteni és rajzos formában rögzíteni. A kalandozások egyre távolabbi vidékek rajzos megjelenítését vonta maga után. A viszonylag kis távolságok esetén (néhányszor 10 km) a térkép síkbeli megjelenítése kis hibát jelent, de nagyobb területek megjelenítése során a rajzos megjelenítés torzított. A teljes Föld bolygó síkbeli ábrázolása úgynevezett vetítéssel, projekcióval képezhető sík lapra [1]. A síkra vetítés komoly szerkesztési feladat volt, de manapság a számítástechnika fejlődésének eredményeképpen ez a feladat a korábbi gyakorlatokhoz képest egyszerűen megvalósítható. Ilyen vetítési megoldást biztosít a MATLAB program is [4], ahol a - Mapping Toolbox--ban több mint 50 féle vetítési módszer közül választhatunk. A következő MATLAB programrészlet a szinuszos (sinusoidal) vetítést mutatja be. Adatbázisként a Mappind Toolbox - coast.mat - fájlt használjuk:
A futtatás eredménye a következő:
1. ábra Sinusoid Az előző esetben megjelenített adatokat, most - Mercator - vetítéssel képezzük le:
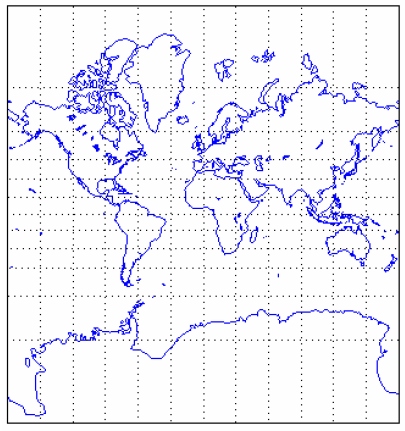
A futtatás eredménye a következő:
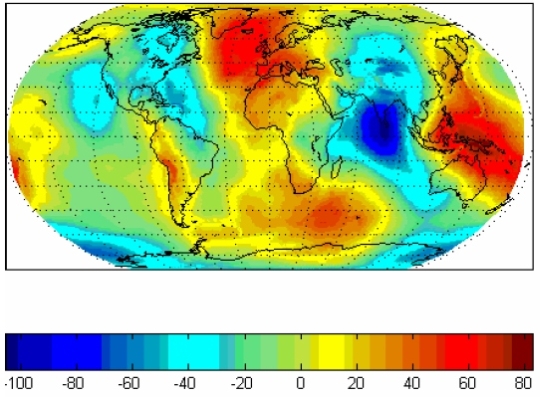
2. ábra Mercator A magasságmérés és magasság meghatározás referencia felületének a geoid-et alkalmazzuk. A geoid egy olyan ekvipotenciális felület, mely minden pontjában a nehézségi erő merőleges a felületre, vagyis ha bármely pontját vizsgáljuk, akkor a nehézségi erő a geoid bármely pontjára helyezett pontszerű testen nem hoz létre elmozdulást, vagyis nem végez munkát. A Föld általános (úgynevezett generalizált) felszínét ellipszoiddal közelítjük [1] [6.]. Az ellipszoid pontjai általában eltérnek a geoid felülettől. Ezt mutatja be szemléletesen a következő MATLAB példa:
A futtatás eredményeképpen a következő ábrát láthatjuk:
3. ábra Geoid és ellipszoid eltérése méterben A geoid és az ellipszoid közti eltérést az ábrán különböző színekkel jelöltük. Korábban a magyarországi katonai térképek Kraszovszkij-ellipszoidra vonatkoztak és Gauss-Krüger vetületben készültek. A magyarországi polgári térképészet az IUGG-67 ellipszoidot alkalmazta. Hazánkban manapság az úgynevezett Egységes Országos Vetületi Rendszert alkalmazzuk, melynek alapját a HD72 dátum képezi [6]. A NATO és a Magyar Honvédség az UTM vetületi rendszert használja MGRS koordináta rendszerben. A térképezéshez felhasznált koordináta rendszereket geodéziai dátumnak nevezzük. A használt geodéziai dátumok országonként eltérőek lehetnek. Észak Amerikában NAD27 és NAD83 dátumot használják, míg Európában az EUREF-et. Az Amerikai Egyesült Államok katonai felhasználásra az úgynevezett WGS-84 (1984 World Geodetic System ) dátumot alakította ki [2] [6] [7]. Napjainkban a papír alapú térképeket nagyrészt leváltották a digitális térképek. A polgári élet hétköznapjaiban is egyre inkább digitális térkép alapján tájékozódunk, gondoljunk a PDA-n, vagy mobiltelefonon futó szoftverekre (iGO vagy Destinator). A térinformatikában az adatok tárolására több adatmodell is szóba jöhet. A legelterjedtebben alkalmazott adatmodelleket két nagy csoportba sorolhatjuk [2] [3] [5] [6]:
A vektoros modell esetén az ábrázolandó két- vagy háromdimenziós tér pontokból és a pontokat összekötő vektorokból áll. A digitális tér reprezentáció vektoros modell esetén is sokféle lehet. Ezek közül a legfontosabbak a következők [6] [7]:
A tesszelációs adatmodell esetén a megjelenítendő, vagyis a digitális térbe leképzendő geometriai elemeket szabályos-, vagy szabálytalan sokszögekkel történő rekurzív felbontással adjuk meg [6]. Legismertebb tesszelációs modell a négyzethálós modell (grid vagy raszter). A négyzethálós modell elterjedésének fő oka az, hogy az adatok tömbben, vagy mátrixban szemléletesen tárolhatók. Háromdimenziós digitális leképezés esetén a domborzat is rögzíthető. A domborzati modell a digitális leképezés során rögzített felbontással adja meg a felszín magasságokat. Jelenleg a domborzat feltérképezésének legmodernebb technikája az SRTM (Shuttle Radar Topography Mission). Ezt a radar technikán alapuló feltérképezést műholdakról végzik [11]. SRTM segítségével térképezték fel a Mars és a Vénusz felszínének részeit is a Mars és a Vénusz expedíciók során. A Föld domborzati modell (DDM) fejlesztés az adott ország nemzeti geodéziai, térképészeti szolgálat feladata. Egységes domborzati modell 1999-ben készült. Az Amerikai Egyesült államok GLOBE modellje (Global Land One-kilometer Base Elevation model) a Föld felszínét egy kilométeres felbontásban ábrázolja. A GLOBE modell Interneten szabadon elérhető, letölthető [11]. A Föld SRTM mérések 2000 február 11-én indultak (NASA Endeavour), és a mérések feldolgozását 2004 közepén fejezték be. A mérési adatokból elkészített adatbázis szintén ingyenesen letölthető. [12] A letölthető fájlok - hgt- kiterjesztésűek. Az adatmodell BIL (Band Interlaved by Line) formátumú. A térképek a WGS-84 dátumhoz igazodnak. Navigációs, helyzet-meghatározó rendszerek Napjaink leghatékonyabb és legolcsóbb helymeghatározó rendszere a GPS. A GPS rendszerek használata általános felhasználás esetén díjmentes. Helymeghatározás tekintetében a jelenleg használatos rendszerek pontossága kielégítő, a helyzet néhány méteres pontossággal meghatározható. A térinformatikai adatbázisban műholdas helyzet-meghatározó rendszer segítségével a robot helyzete egyszerűen leképezhető a virtuális digitális térbe. A digitális térben az autonóm robot, mint 3D objektum ábrázolása sok esetben egy pont. A pont aktuális helymeghatározása a digitális térben tehát GPS-szel történhet. A műholdas helymeghatározás időmérésre visszavezetett távolságmérésen alapul. A rádióhullámok terjedési sebessége ismeretében a meghatározandó pont távolsága az adott mérőjelet szolgáltató műholdtól kiszámítható [7] [9]. A kiszámított távolság egy adott mérőjelet szolgáltató műholdtól a számított távolsággal megegyező sugarú gömbfelületet definiál, mely gömb középpontja maga a műhold. Egy másik műholdról érkező mérőjel észlelése esetén az előzőekhez hasonlóan szintén egy gömbfelületet kapunk. A két gömb metszi egymást, a metszetük egy kör lesz. A meghatározandó pontunk (vagyis a helyzetünk) a kapott körön helyezkedik el. Egy további (harmadik) műhold esetén is elvégezzük a távolság számítást, akkor ismét egy gömböt kapunk, mely gömb ismét metszi az előző gömböket. A helyzetet a közös metszéspont fogja jelenteni. A fenti gondolatmenet csak a működés elvét szemlélteti. Az alapelv sok gyakorlati buktatót rejt, ugyanis pontosan ismernünk kell a rádióhullámok kibocsátásának és a vevőbe érkezésének idejét. Az időmérésnek nagy pontosságúnak kell lennie, mivel a mérőjel futásideje (műholdtól a vevőig) átlagosan 0,06 másodperc. Abban az esetben, ha az időmérésünket 0,001 másodperces (1ms) hiba terheli, ez 300 km helyzet meghatározási pontatlanságot jelent. Ez okból a műholdakon nagy pontosságú (10 -12 10 -13 pontosságú, rövid idejű frekvencia stabilitású) atomórák működnek. A vevőben ilyen pontosságú órát elhelyezni nem lehet, elsősorban az ára miatt. A vevőben egyszerű kristály oszcillátoros óra üzemel, mely óra a műhold által sugárzott jel segítségével a műhold órájára szinkronoz. Természetesen a szinkronizálás csakis konstans hibával történhet a jel terjedési sebessége miatt. A konstans hiba kiejthető, ha egy negyedik műhold jelét is vesszük, vagyis a gyakorlatban a GPS vevő akkor szolgáltat viszonylag pontos koordinátákat, ha az egyszerre legalább négy műhold jelét veszi. Az amerikai NAVSTAR rendszer 24 darab 12 órás keringési ciklus idejű műholdból áll. A műholdak hat pályasíkon, egymástól 60 fokkal elforgatva keringenek. A Föld egyenlítőjéhez viszonyított pályaelhajlás 55 fok. A műholdak keringési magassága 20200 km . A földi felügyelő állomás öt helyen működik, négy feltöltő és egy központi vezérlő segíti az üzemeltetést. Az amerikai NAVSTAR GPS rendszert napjainkban több millió ember használja mind civil, mind katonai területen. A NAVSTAR rendszer üzemeltetése katonai kézben van. A felhasználók több ponton kiszolgáltatottak, hiszen ha a tájékozódásukat erre a rendszerre építik, akkor a rendszer - kikapcsolása-, - lekódolása- vagy szándékos jel - torzítás- a tájékozódást lehetetlenné teszi. Ez a tény nagy mértékű kiszolgáltatottságot jelent, ezért a tenger hajózás és a repülés területén a GPS használata csak egyéb kiegészítő navigációs rendszerekkel együtt lehetséges. Az Európai Unió ettől a kiszolgáltatottságtól kíván szabadulni és ezért saját GPS rendszer kialakítását, és üzemeltetését tervezi [8]. Nemrég bocsátották fel az európai Galileo navigációs rendszer első kísérleti műholdját (Giove-A). A kilövés a kazahsztáni Bajkonúr űrközpontból történt, a hordozó rakéta Szojuz volt. A kísérleti hold 23260 km magasságban kering, keringési ideje 14 óra 22 perc. A kísérleti méréseket az angliai Chilbolton obszervatóriumban végzik. A Galileo GPS rendszer üzembe állítását eredetileg 2008-ra tervezték, de ez várhatóan csak 2010-ben fog megtörténni. GPS koordináták bizonytalansága A GPS vevő által meghatározott koordináták sok esetben bizonytalanságot mutatnak, az egyes számított eredmények hibával terheltek [10]. A hiba okai a következők lehetnek:
Az Ionoszféra futásidő torzítása viszonylag állandó, ezért az korrekciós számításokkal viszonylag jól kiküszöbölhető. A fenti vételi problémák közül talán a legnehezebben a Troposzféra, mint időjárásfüggő torzítás jelentkezik. Az időjárásfüggő hiba nehezen korrigálható, gyakran az erősen felhős időben teljes, vagy részleges vétel kiesés is előfordulhat. A robotkutatások során a koordináták hihetősége, valamint a hihetőség vizsgálat nagy jelentőséggel bír. Hihetőség vizsgálat legegyszerűbb esete a következő: Tételezzük fel, hogy a robotra rögzített GPS vevő másodpercenként szolgáltatja a vevő helyzetére jellemző koordinátákat. A robot v sebességgel halad. A v vektoriális mennyiség, melyet a GPS vevőtől független szenzorokkal detektálunk. A v · t = s összefüggésből (itt most skalár mennyiségekkel számolunk, ahol v a v abszolút értéke) számíthatjuk az egy másodperc alatt megtett utat. A GPS adatok koordinátáiból szintén számítható a megtett út. Nagy eltérések esetén a mérési eredményeket fenntartással kell fogadni, azokat útvonal korrekcióra azonnal felhasználni nem szabad. A fentiekből jól látszik, hogy a szenzorok többszörös tartalékolása az autonóm robotok esetében (például pilóta nélküli repülők – UAVk ) elengedhetetlen. A szenzor eredmények fúziója növeli a megbízhatóságot. Pontosság növelő tényező lehet az egyes mérési eredmények átlagolása. Az átlagképzés integráló hatása zaj- és mérési hibacsökkentő. GPS vevő modul Napjainkban, a kiskereskedelmi forgalomban számos, jó minőségű, kis méretű GPS vevő modul vásárolható. A vevő modul az alkalmazott csúcstechnikának köszönhetően olcsó tömegcikknek tekinthető. A továbbiakban egy olyan GPS vevő modult (FALCOM JP7) mutatok be, mely a robotkutatások során nagy sikerrel alkalmazható [9].
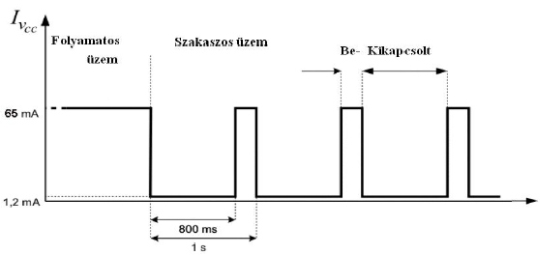
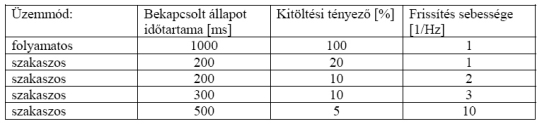
4. ábra GPS vevő modul A 4. ábrán látható vevő modul mérete 25 ,4 x 25,4 x 3 mm . A modul SMD alkatrészként ültethető be az alkalmazásba. A tömege árnyékoló lemez nélkül körülbelül 2,5 gramm. A széles működési hőmérséklet tartomány (-40 oC - +85 oC) lehetővé teszi a kis méretű pilóta nélküli repülőkön történő alkalmazását. A mechanikai rögzítés során ugyanakkor figyelembe kell venni, hogy a modul maximum 20 m/s sebességű rázkódást és 4g gyorsulást képes elviselni meghibásodás nélkül. A GPS vevő modul által szolgáltatott koordináták pontossága 10 méter, DGPS esetben ez az érték 1-5 méteres pontosságon belüli [9]. A számított objektum sebesség pontosság 0,1 m/s, míg differenciális módban ez 0,05 m/s pontosságúra finomodik. A GPS vevő belső órája 1 µs pontossággal szinkronoz. További előnyként kell megemlíteni a csökkentett teljesítmény felvételi üzemmódot. Korábbi cikkemben számoltam be a pilóta nélküli repülők elektronikai tápellátás kérdéseiről és az elektromos energia hatékony felhasználásáról [13]. Az 1. ábrán látható modul támogatja a szakaszos működést, ezzel az átlagos teljesítmény felvétel (áram felvétel) jelentősen csökkenthető:
5. ábra GPS vevő modul áramfelvétele az idő függvényében A FALCON JP7 vevő modul áramfelvétele 3,3 V tápfeszültség esetén folyamatos működés esetén maximálisan 65 mA. Abban az esetben, ha koordinátákat csak másodperc gyakorisággal várunk a modultól, akkor minden egy másodperces ciklusban az idő 80%-ban a vevő modul alacsony tápáram felvételi (készenléti) üzemmódba kapcsolható, ami átlagosan csaknem 80% teljesítményfelvétel csökkenést jelent. A FALCON JP7 modul például a következő üzemmódban használható [9].:
1. táblázat Példa néhány működési üzemmódra Ha a GPS vevőt bekapcsoljuk, akkor az megkezdi az aktuális pozíció, sebesség meghatározását, valamint szinkronizálja az óra áramkörét. Az átmeneti adatok (Ephemeris Data - gyors elévülési idejű adatok) begyűjtése után a GPS vevő a műholdak jelét folyamatosan követi és a koordinátákat ciklikusan számolja. A helyes pozíció meghatározásához minimum négy műhold jelének vétele szükséges. A vett és kalkulált adatokat a GPS vevő a belső SRAM-ban tárolja. Az SRAM-ban tárolt adatok aktualitása szerint a bekapcsolás utáni indulás kétféle lehet:
"Hot start" esetén a belső SRAM-ban az előző mérések eredménye még megtalálható és azok még részben aktuálisnak tekinthetők. Ennek feltétele az, hogy ne történjen jelentős mértékű pozíció változás a kikapcsolt állapot alatt. Pozíció változásnak tekintendő ebben az esetben a műholdak keringése is, vagyis a kikapcsolt állapot időtartama is meghatározó, nemcsak a GPS vevő pozíciójának megváltozása. A "hot start" körülbelül 8 másodperces időt jelent. Hideg indítás ("Cold start") esetén előző mérési eredmények nem állnak rendelkezésre, vagy azok már teljesen elévültek. Ekkor az indítási idő körülbelül 45 másodperc. A GPS vevő a mérési eredményeket és az abból számított koordinátákat soros kommunikációs interfészen juttatja el a feldolgozó számítógéphez, például a robotpilótához. A FALCOM JP7 GPS vevő modul két egymástól függetlenül működő soros kommunikációs interfésszel rendelkezik, mely CMOS szintekkel működik. Személyi számítógép (PC) soros aszinkron porthoz (V.24, RS-232) csatlakoztatás csak szintillesztő áramkör közbeiktatásával lehetséges. A soros interfész csatlakozási pontjai a GPS vevő modulon a következők:
Az interfészeken két elterjedt és általánosan alkalmazott protokollal történhet a kommunikáció:
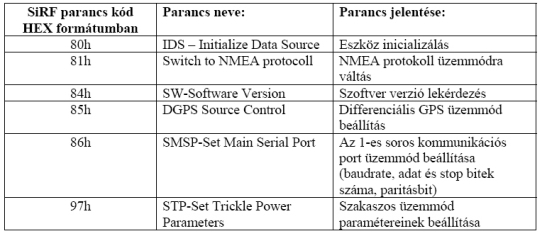
A SiRF binárisan adja a pozíciót, sebességet, magasságot és státuszt. Az egyes mezőket a SPACE karakter (20h) választja el. Néhány fontos SiRF parancsot a következő táblázatban láthatunk [9]:
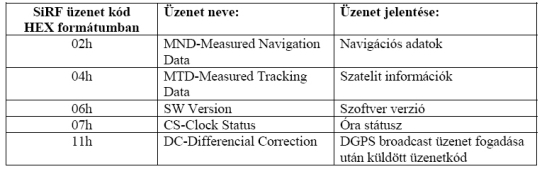
2. táblázat A FALCON JP7 modul néhány SiRF parancskódja Néhány fontos SiRF üzenetet a következő táblázatban láthatunk [9]:
3. táblázat A FALCON JP7 modul néhány SiRF üzenetkódja Az NMEA protokoll a GGA, GLL, GSA, GSV, RMC és VTG üzenetformátumokat támogatja. Az NMEA kimenő üzenetek összefoglalóját a következő táblázatban láthatjuk [9]:
4. táblázat A FALCON JP7 modul néhány NMEA üzenetkódja A térinformatikai rendszer és a GPS vevő tehát soros aszinkron vonalon kapcsolódhat. A kommunikációs vonalon keresztül bizonyos időközönként átadásra kerül a robot helyzete és az egy pontként jelenik meg a virtuális digitális térben. A robot mozgására és irányítására születő döntések tehát a virtuális térben történnek meg. A virtuális tér pontossága és aktualitása fontos tényezője az autonóm robotok helyes működésének. Összegzés Korunkban a robotkutatások nagy ütemű fejlődését elsősorban az tette lehetővé, hogy a memóriák mérete és tároló kapacitása, valamint a processzor egységek utasítás végrehajtó képessége nagymértékben megnőtt. A robotkutatások elválaszthatatlan módon összekapcsolódtak több, eddig egymástól szeparált kutatási területtel, így a térinformatikával is. Napjaink és a jövő robotjai komplett térinformatikai rendszerek szállítóivá válnak, fedélzetükön térinformatikai adatbázisokat szállítanak és valós időben dolgozzák fel a térinformatikai adatokat. A robotok megfigyelése, kezelői, felügyelői követése szintén digitális térképen történhet. A jövő robotjai nemcsak a térinformatikai adatok felhasználói, hanem azok szerkesztői is, működésük közben megtanulják, "megismerik" a működési környezetüket és azt pontosan leképezik a térinformatikai adatbázisukba.
Felhasznált irodalom [1] Sebők István GPS alapú korszerű navigálási eljárások és eszközeik c. könyv első fejezete: "Geodéziai és geográfiai ismeretek összefoglalása" [4] MATLAB Mapping Toolbox; www .mathworks .com [5] Haig Zsolt, Elektronikai harc térinformatikai adatbázisa, Magyar Hadtudomány Társaság folyóirata 1996. 4. sz . 75-83. [6] Detrekői Ákos - Szabó György Bevezetés a térinformatikába 1995. Budapest, Nemzeti Tankönyvkiadó [7] http://terinformatika.geocentrum.hu [8] Frey Sándor, Galileo 2006 .03 .18 . www.urvilag.hu [9] JP7_T_Family_1.05.pdf www.falcom.de [10] Pázmányi Sándor, Dobos Attila, Pajna Sándor, A GPS-es helymeghatározás pontossági kérdései és alkalmazási lehetőségei a mezőgazdaságban. [11] Timár Gábor és Kohán Balázs, Digitális domborzatmodell az űrből; www.gpsmagazin .hu [12] ftp://e0srp01u.ecs.nasa.gov/srtm [13] Wührl Tibor, Mikro méretű pilóta nélküli repülők repülésbiztonsági kérdései - elektromos tápellátás biztonsága; 2006 Szolnok |
© ZMNE BJKMK 2006.