Absztrakt A térinformatikai szoftverek egyre szélesebb köre képes kezelni a digitális magassági modelleket. A felhasználók egyre többféle, különböző módon előállított digitális magassági modellekhez juthatnak hozzá. Ahhoz, hogy ki tudjuk választani a megoldandó feladat igényeit kielégítő digitális magassági modellt, szükséges ismerni azok előállítási technológiáit és minőségi paramétereit. A nem megfelelő tulajdonságokkal rendelkező adatbázisok téves, vagy hibás következtetéseket, eredményeket szolgáltathatnak. Ezért fontos ismerni a digitális magassági modellek jellemzőit, fő pontossági mérőszámait. Increasingly wider range of the GIS softwares can handle digital elevation models. The users could come by increasingly various digital elevation models, made by different methods. For choosing the right digital elevation models, you need to know their production techniques and quality parameters. The databases, which have no suitable characteristic, could result in false or erroneous conclusion, effects. So, you need to know the characteristic qualities, main accuracy indexes of the digital elevation models. Kulcsszavak: magassági modell, Digitális Domborzat Modell, DDM, DFM, DSZM,
BEVEZETŐNapjainkban a technika fejlődésének hatására a gazdaság mind több ágában - térképészettel kezdve, a külszíni bányászaton, a mezőgazdaságon, a telekommunikációs és egyéb infrastrukturális hálózatok tervezésén és üzemeltetésén át a honvédelmi és katasztrófa-elhárítási feladatok végrehajtásáig - a napi gyakorlati munkához igénylik a Föld felszínének, domborzati viszonyainak mind pontosabb, megbízhatóbb és naprakész ismeretét. A Föld felszínének bonyolultsága és méretének nagysága nem teszi lehetővé, hogy egy, matematikailag viszonylag könnyen kezelhető függvénnyel leírjuk. E probléma megoldására több eljárást dolgoztak ki:
A már létező és kialakítandó adatbázisok meghatározásakor - adatstruktúrális és kezelhetőségi szempontokat is figyelembe véve - elsősorban a szabályos elhelyezkedésű, diszkrét pontokkal való felületleírást alkalmazzák. Az ország területéről ilyen 10×10 méteres felbontású Digitális Domborzat Modellel (továbbiakban DDM) már rendelkezik a Honvédelmi Minisztérium Térképészeti Közhasznú Társaság (továbbiakban HM TKHT) (Sass, 1993) . A Földmérési és Távérzékelési Intézetben (továbbiakban FÖMI) jelenleg folyik az ország teljes területét lefedő, 5×5 méteres rácsméretű DDM végleges kialakítása (Iván, 2000). (A domborzati fedvények nyers és sztereofotogrammetriai módszerrel javított vektorizált változatát már szolgáltatják.) A DIgitális Topográfiai AdatBázis (továbbiakban DITAB) szabványkézirata (Magyar Szabvány MSZ 7772-2T: 2000) a rácscellák oldal-hosszúságát 5-30 méterben - a terep jellemzőitől függően - határozza meg. Cikkemben összefoglalom a térinformatikai alkalmazások által alkalmazott digitális terepmodellek előállítási technológiáinak jellemzőit, valamint a térinformatikai adatok minőségvizsgálatának folyamatát. DIGITÁLIS MAGASSÁGI MODELLEKA DDM-k előállítási technológiáinak tárgyalásához szükséges a különböző magassági adatrendszer fogalmak tisztázása. Az MTP a DITAB-hoz kapcsolódóan a következő magassági adatrendszereket különbözteti meg (Bakó 1999):
A megfogalmazásokból kitűnik, hogy a DDM és DSZM között adatstruktúrális, DDM és DFM között pedig adattartalmi különbségek vannak. A DDM létrehozásának folyamatát három fázisra tagolhatjuk (Divényi 1986):
Az adatgyűjtés a DDM létrehozásához szükséges elsődleges adatok (elsődleges adatmodell) nyerését jelenti. A modellezés két részfolyamatból, a modellépítésből és a modellkiértékelésből áll össze. A modellépítésen az elsődleges adatmodell adatai közötti kapcsolatrendszer kialakítását, a modellkiértékelésen a DDM másodlagos adatmodelljének felépítését értjük. Ennek megfelelően a modellkiértékelés foglalja magába az interpolációs és approximációs módszereket, az információt előállító eljárásokat és ezen folyamatok eredményeit megjelenítő algoritmusokat is. Az eredmények felhasználásának témaköre felöleli a kialakított DDM alkalmazásának lehetséges formáit, mint például ortofotó készítés, szintvonalszerkesztés különböző méretarányokban való megjelenítéshez, lejtőkitettségi térkép, hossz- keresztszelvények előállítása, összelátásvizsgálat stb. Digitális Domborzat Modellek előállítása A DDM elsődleges adatmodellje háromféle mérési technológiával állítható elő:
Az előállítási eljárások domborzatmodellezési szempontból lényeges jellemzői a következőkben foglalható össze.
Eljárásai a topográfiai felmérés (tachimetria, GPS) és a területszintezés (magasságilag jellegtelen területen). A topográfiai felmérés, technológiájából adódóan adatszerkezete szabálytalan, szórt ponthalmazra vonatkozó: Psz, y, x, z, kód. A területszintezés szabályos rácsháló mentén történik így adatszerkezete:
A fejrész adja meg a rácsháló helyzetét, irányát, felosztását és méretét. A felmérés pontosságát a mérési eljárás és műszerek, illetve a bemért pontok azonosítási megbízhatósága befolyásolja. Az adataiból generált DDM megbízhatóságát a bemért pontok pontossága és sűrűségeloszlása befolyásolja. Használata nagyobb terület felmérése esetén idő- és költségigényes, ezért csak kivételes esetekben célszerű alkalmazni (ÁFTH 1966). Alkalmas közvetlenül DDM és DFM, közvetve DSZM előállítására.
Kiértékelési technológiái:
Az elmúlt években kerültek bevezetésre a korszerű digitális magasságmérő technológiák. Ezek alkalmazhatók mind repülőgépek (LIght Detection And Ranging - LIDAR , InterFerometric Syntetic Aperture Radar - IFSAR), mind műholdak (Shuttle Radar Topographic Mapping - SRTM) fedélzetéről. A pásztázó leképzési módszer megköveteli az utólagos feldolgozást (Davis, 2004). Nagy területek mérhetők fel rövid idő alatt. Elsődleges adatfelépítése szórt pontos, utófeldolgozás után szabályos rácsháló:
Pontosságát az adott technológia paraméterei határozzák meg. Kisebb pontosságú változatai (pl.: 3x3 másodperces [75x90 m] rácshálóban) ingyen hozzáférhetők. Az eljárással , az alkalmazott hullámhossz függvényében DFM, vagy DDM állítható elő
Meglévő térképi alapok feldolgozását, szintvonalrajzának digitalizálását, vagy domborzati fóliájának szkennelését jelenti.
Adatfelépítése célszerűen: z, y1 , x1 , y2 , x2 , .yi , xi , végjel, illetve: yi , xi , zi . Látszólag ez is szórt pontállomány, de sűrűségeloszlása nem egyenletes, ami a további feldolgozásnál problémát okozhat.
A térkép domborzatrajzi oleátájának szkennelése során gondot okozhat az alapanyag minősége (háttérzaja), tartalmi hiányok (megszakítások) valamint többlet információk (jelkulcsi elemek) jelenléte. A hiányosságok korrigálása általában manuális javítással történik (Katona E. 1995). Az így megjavított raszteres adatállomány további feldolgozása történhet raszteres, vagy vektoros technológiával. A kartometriai eljárások pontosságát a feldolgozandó térkép ábrázolási megbízhatósága, az alapszintközeinek távolsága és a digitalizáló eszköz pontossága, illetve a szkennelés felbontása határozza meg. Ebből adódóan - mivel levezetett adatokat alkalmaz - megbízhatósága kisebb. Aktualitása a térkép felmérési idejére vonatkozik. Költségigénye alacsony. Megfelelő minőségű alapanyag használata esetén jól automatizálható. Adatszerkezetében az idomváz felépítése nem tárolható. Alkalmas közvetlenül DSZM, közvetve DDM, attribútumadatok felhasználásával DFM előállítására.
Fontosabb térbeli interpolációs és approximációs eljárások A térbeli interpolációk alkalmazási köre sokrétű:
"Térbeli interpoláció az az eljárás, amely a rendelkezésre álló megfigyelések által meghatározott térség mintavétellel nem rendelkező pontjaiban becslést ad a vizsgált tulajdonságok értékére. . A térbeli interpoláció azon feltevésen alapul, hogy a térben egymáshoz közel elhelyezkedő pontok értéke nagyobb valószínűséggel hasonló, mint az egymástól messze lévő pontoké (bler törvénye a geográfiára)" (Závoti J. 1994). Az idézett megfogalmazás tömören és lényegre törően összegzi a térbeli interpoláció feladatát és megoldásának elvét. A feladat végrehajtása sajnos nem ilyen egyszerű. A térbeli interpoláció megvalósítására, mint az interpolációkra általában többféle eljárást dolgoztak ki.
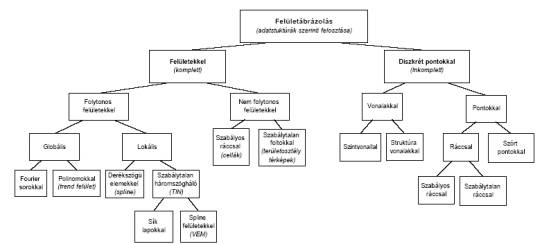
A térbeli interpolációs algoritmusok több szempont alapján is csoportosíthatók:
1 . ábra: A térbeli interpolációs eljárások adatstruktúra felépítésén alapuló felosztása
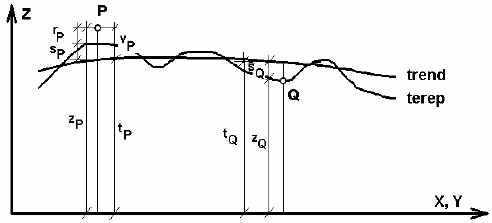
Ha megmérjük egy időben állandó sztochasztikus folyamat egyes pontjaihoz tartozó értékeket (zP), a folyamatot leíró trendfelület a S(vv) = minimum feltétel mellett meghatározható. A zP érték vP javítása a mérést terhelő sP szabályos hibára (jelre) és rP véletlenjellegű hibára (zajra) bontható fel (2. ábra): zP = tP +vP = tP +sP +rP . Így egy új pont értéke meghatározható:
2 . ábra: Legkisebb négyzetek módszerén alapuló kollokáció
A diszkrét adatstruktúrára épülő legegyszerűbb interpolációs eljárásokat a dinamikus felületek kel való közelítés szolgáltatja. Lényege, hogy minden új pontban új felület meghatározásából ad becslést. A felület lehet vízszintes sík, ferde sík, vagy másodrendű polinom. Általános egyenlete: A felület típusa a számításba bevont tagok számától függ. Legegyszerűbb közelítés (csak az a00 tag figyelembevételével) a vízszintes sík . A sík a környező pontok súlyozott középértéke, a meghatározott felület lépcsős (a szomszédos felületelemek között az átmenet függőleges). Jobb eredményt szolgáltat a ferde sík kal való közelítés. E két eljárás adatszükséglete viszonylag alacsony, de érzékeny a pontsűrűség-eloszlási anomáliákra. A másodrendű polinom mal előállítható felület a terep görbületeihez még jobban illeszkedik, de jóval több pontot igényel. Információhiányos területen, vagy a terület széleinél a felület a tereptől erősen eltérhet, nem valós domborzati viszonyokat adhat eredményül (a felület "belenghet"). Az együtthatók meghatározását célszerű több ismert pont felhasználásával súlyozva, a legkisebb négyzetek módszere alapján kiegyenlítéssel meghatározni. Az eljárás minimális pontigényét az alkalmazott felület típusa (fokszáma) határozza meg:
A dinamikus felületek módszere technológiájából adódóan, nagyobb területre kiterjedő interpolációs módszer, ezért a helyi, gyors változások visszaadására nem képes. A helyi viszonyok kifejezésére alkalmasabb eljárások a polinomfelületek et alkalmazó interpolációk. Lényegük, hogy a terepet az adatszerkezetből eredő legkisebb felületelemre (szabályos adatstruktúra esetén rácshálószemre, szabálytalan adatstruktúra esetén háromszögű hálószemre) meghatározott polinomfelületekkel közelítik. A gyakorlatban első-, másod-, és harmadrendű polinomokat használnak. Magasabb fokú polinomok alkalmazását mellőzik a meredeken növekvő adatigény (p 2), és az előző eljárásnál már említett "belengés" miatt. A polinomfelületekkel interpoláló algoritmusok alapképlete a következő biköbös polinomösszefüggés:
A polinom paraméterértékeinek meghatározása a támpontok magassági, és egyéb, a lejtésviszonyokra jellemző adatai alapján történik (Divényi 1986). A meghatározott felület, szabályos rácshálós adatszerkezet esetén, x és y koordinátatengely irányú metszetei harmadfokú polinomgörbék, ugyanakkor két szomszédos polinomfelület x = konstans, illetve y = konstans csatlakozás mentén, azonos tereplejtési adatokkal rendelkezik x, illetve y irányban. Ezért ezt az eljárást főként szabályos adatstruktúrájú, szabályos rácshálós adatszerkezetű felületmodellek interpolációs feladatainál alkalmazzák. A biköbös polinomösszefüggésből egyszerűsítésekkel levezethető a 4 tagú bilineáris polinomösszefüggés:
Ez a polinomfelület a hiperbolikus paraboloid, más néven nyeregfelület, amely négy rácshálópont magassági értékeire illeszkedik. A bilineáris interpoláció térképészeti célú felhasználása nagy jelentőséggel bír.
A raszteres interpolációs eljárások közös tulajdonsága, hogy a számítási algoritmus nem túl bonyolult, de megfelelő eredményt csak többszörös iteráció után szolgáltatnak, ezért időigényes metódusok. Az egyik alkalmazott metódus a membrán modell eljárás. Az iteráció menete két részre bontható. Az első lépés a kezdő-értékadás , amikor valamilyen rendszer szerint minden raszterponthoz hozzárendelnek egy előzetes magassági értéket. (Az előzetes és a valódi érték különbsége hatással van az iteráció lépésszámára). Ezt követi a relaxáció (iteráció), melynek folyamán lokális szomszédsági műveletek végrehajtásával (a négy szomszédos elem átlagának képzésével), a szintvonalak értékének rögzítésével az iterációt addig végzik, amíg megfelelő domborzatot kapnak. Ez az eljárás a szintvonalak közé minimális felszínű felületet feszít ki. A fentiekből következik, hogy ez az eljárás szintvonalhiányos (sík) területen meglehetősen lassú, és a terep domborzati viszonyait nem képes helyesen visszaadni (a szintvonalak mentén törések léphetnek fel, a lokális minimum, maximumhelyek eltűnnek, sík területté alakulnak át). A membrán modell lassúságát küszöböli ki a multigrid technika . Elve a digitális képfeldolgozásban ismert képpiramis technikához hasonló. A mátrix előzetes értékeinek meghatározása egy erősen lecsökkentett felbontású mátrixból, redukált DSZM mátrixból kiindulva a felbontás fokozatos növelésével történik. Így eredményül lényegesen jobb előzetes értékeket kapunk, ami az iteráció lépésszámát nagyságrendekkel lecsökkenti. Azonban a membrán modell domborzatmegjelenítési hibáit ez az eljárás nem szünteti meg. E hiányosságot küszöböli ki a vékony lemez-modell (thin plate) eljárás. Ez a módszer az előzőekkel ellentétben minimális görbületi energiájú felületet állít elő. Így a szintvonalaknál jelentkező törések megszűnnek és a lokális minimum, maximumhelyek is megjelennek. Az eljáráshoz az előzetes értékeket a multigrid eljárással szolgáltatják. Az iterációs eljárás során a szomszédos raszterpontok x és y irányú differenciáinak minél egyenletesebb változását biztosítják (közel számtani sorozatot alkossanak). Ez szemléletesen azt jelenti, hogy egy 5×5 raszterelem méretű szűrő maszkkal végzik az egyes elemek magassági értékének meghatározását (Katona E. 1995). A szűrő maszk A Digitális Domborzat Modellek előállításának vizsgálatakor "megállapítható, hogy pontosságot elsősorban a terepfelszín jellege és a mért támpontok minősége (pontossága, elhelyezkedése), illetve mennyisége határozza meg. Az interpolációs módszer megválasztása lényeges lehet az eredmény kartográfiai minőségére, de a pontosságra csak kis hatással van" (Divényi 1986). A TÉRINFORMATIKAI ADATOK MINŐSÉGI MÉRŐSZÁMAIA térinformatikai adatok minőségi mérőszámai vizsgálatának elkezdése előtt célszerű tisztázni a minőség fogalmát. "Minőség: a termék azon jellemzőinek összessége, amelyek a meghatározott és elvárt igényeknek való megfeleltetés mértékét befolyásolják" (Detrekői Á. - Zöld S. 1999). A térinformatikai adatok minőségét befolyásoló legfontosabb tényezők (Detrekői Á. - Szabó Gy. 1995): - az adatok eredete;
Így ezen adatok minőségvizsgálatához a fent felsorolt összes információ és adat együttes analizálása szükséges. Az adatok minőségének jellemzőit kifejezhetjük szöveges leírás sal, vagy számszerű mennyiségekkel. A szöveges jellemzés foglalja össze az adatok eredetével, teljességével és az aktualitással kapcsolatos információk nem számszerűsíthető részét. Az adatok eredetének felkutatásakor célszerű az alábbi információk felkutatása:
A numerikus minőségi jellemzők tájékoztatást adnak:
A pontosság az adatok mért és elméleti értékének eltérését adja meg. Mérőszáma a középhiba (szórás) és az eltérés. Az adatok élesség ét az adatok megadott tizedesjegyek száma jellemzi. Az élességnek és a pontosságnak összhangban kell lenniük. A megbízhatóság ot az adatállományban már kimutatható legkisebb durva hiba értéke fejezi ki. A megbízhatóság kapcsolatban van a pontossággal, de nem azonos azzal. Az adatok teljesség e az adatbázis objektumai és a valóság közt fennálló kapcsolatot minősíti. Az aktualitás az adatbázis változásának várható mértékére, így adattartalmának helyességére ad ismereteket (Detrekői Á. - Zöld S. 1999).
A Digitális Domborzat Modellek minőségvizsgálata a térinformatikai adatok minőségvizsgálatáéhoz hasonló folyamat, de egyedi jellemzőiből adódóan a pontossági mérőszámok meghatározása, vizsgálata és értelmezése speciális szempontok figyelembevételét igényli ( megszokott eljárások adatigényétől nagyobb az adatszükséglete). A DDM-ek pontossági vizsgálatához nem elegendő a különbségek és az azokból számítható szórás értékének meghatározása. (A későbbi félreértések elkerülése érdekében, a statisztikai adatok tárgyalása során a vizsgált és a referencia DDM differenciáját különbségnek, a különbségek átlaguktól való differenciáját pedig eltérésnek nevezem.) A DDM különbségeinek helyes értelmezéséhez szükséges egyéb statisztikai jellemzők megadása is. Ilyen jellemzők lehetnek (BME Fotogrammetria és Térinformatika Tanszék 2000):
A sűrűséghisztogram alkalmas a különbségek eloszlásának szemléltetésére. A minimális és maximális érték , valamint a terjedelem a különbségek intervallumát jellemzik. A különbségek összege4, átlaga5, mediánja6, módusza,7 Laplace-féle átlagos hibája8 és átlagos eltérése9, megfelelő elemszám esetén, alkalmas a DDM-ben meglévő szabályos hibák kimutatására. Nagy adatbázisú DDM-ek esetén, a kisebb területi elhelyezkedésű szabályos eltérések tisztán numerikus úton való kimutatásához, célszerű az adatbázist megfelelően kiválasztott részterületekre bontani. A DDM-ek pontosságának becslésére a különbségek eltéréseinek szórását10 használják. Az adathalmazban meglévő szabályos hibák kimutatására a A statisztikai számításokkal közvetlenül nincs összefüggésben a különbségek térképi megjelenítése, de azok területi elhelyezkedésének vizsgálatához hatékony módszer. Alkalmazásával kisebb kiterjedésű (kisebb elemszámú), szabályos hibával terhelt adatok is megjeleníthetők, kimutathatók. A szabályos hibák lehetnek a DDM meghatározásából eredőek (mérési hibák, illetve azonosítás következményei), valamint a DDM előállításához felhasznált alapanyagok tartalmi adataiból származtathatók (aktualitásból, illetve az adott adatstruktúrában nem kifejezhető információk elvesztéséből következők). A Digitális Domborzat Modellek minőségvizsgálata a fenti statisztikai jellemzők, és vizuális megjelenítésük együttes elemzésével és értelmezésével ad reális, a DDM valódi minőségére utaló adatokat. ÖSSZEGZÉSAhhoz, hogy a térinformatikai szoftvereink által használt különböző típusú digitális terepmodellek (DDM, DFM) használata során a nyert információkat helyesen tudjuk értelmezni, szükséges ismernünk azok előállítási technológiáinak sajátosságait, műszaki paramétereit. Ezen adatok ismeretében tudjuk eldönteni, hogy az adott domborzati adatbázis megfelelő-e az általunk megoldandó feladat végrehajtására, illetve több adatbázis összevetésével újabb információkat is előállíthatunk.
FELHASZNÁLT IRODALOM ÁFTH (1966): Komplex utasítás az 1:10 000 méretarányú topográfiai térképek készítéséhez. ÁFTH, Bp. Bakó Z. (1999): A Digitális Domborzat Modell meghatározása és létrehozása (MTP). MH TÉHI, Bp. BME Fotogrammetria és Térinformatika Tanszék (2000): 1:10 000 méretarányú EOTR topográfiai térképek domborzati tartalmának ellenőrzése (Összegző jelentés). Bp. Davis P. (2004): Shuttle Radar Topography Mission (SRTM) Technical Guide Detrekői Á. - Szabó Gy. (1995): Bevezetés a térinformatikába. Nemzeti Tankönyvkiadó, Bp. Detrekői Á. - Zöld S. (1999): A DITAB minőségbiztosítása és állami átvétele. (Műszaki szabályzat tervezet) Bp. Detrekői Á. (1991): Kiegyenlítő számítások. Tankönyvkiadó, Bp. Divényi P. (1986): Digitális terepmodellezés a kartográfiában. (Kandidátusi értekezés) Bp. Iván Gy. és munkatársai (2000): Technológiai eljárás az 1:10 000-es méretarányú digitális topográfiai térképek domborzatmodelljének előállítására. FÖMI, Bp. Jones, C. B. (1997): Geographical Information System and Computer Cartography. Longman, Singapore Katona E. (1995): Digitális terepmodell számítása multigrid relaxációs eljárással GK 5 sz. 20-25 o. Magyar Szabvány MSZ 7772-2T: 2000 (2000): Digitális térképek 2. rész: A digitális topográfiai adatbázis meghatározása (Szabványkézirat), Bp. Sass S. (1993): Műszaki leírás az MH TÉHI által előállított Digitális Domborzat Modellről, MH TÉHI, Bp. Závoti J. (1994): Térinformatikai alapismeretek - 40.- 41. fejezet Térbeli interpoláció I-II. NCGIA CC, EFE FFFK Térinformatikai Tanszéke, Székesfehérvár 1 A számhalmaz legnagyobb értéke. 2 A számhalmaz legkisebb értéke. 3 A számhalmaz legnagyobb és legkisebb értékének különbsége. 6 Az az érték, amelynél a valószínűségi változó 0,5 valószínűséggel vesz fel kisebb értéket. A rendezett számhalmaz középső értéke, ha a számhalmazban a számértékek párosan fordulnak elő, akkor a középső két szám átlaga 7 A valószínűségi változó azon lehetséges értéke, melyet nagyobb valószínűséggel vesz fel, mint az egyéb lehetséges értékeit. A számhalmazban leggyakrabban előforduló érték. 10 |
© ZMNE BJKMK 2006.

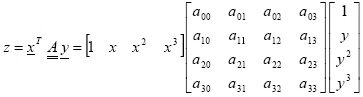 .
. 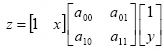
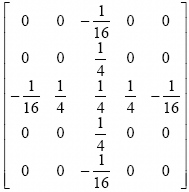 alakú.
alakú. 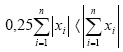 összefüggés alkalmazható (Detrekői Á. 1991). Ha az egyenlőtlenség fennáll, akkor az adathalmazban szabályos hiba megléte valószínűsíthető.
összefüggés alkalmazható (Detrekői Á. 1991). Ha az egyenlőtlenség fennáll, akkor az adathalmazban szabályos hiba megléte valószínűsíthető. 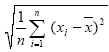 A valószínűségi változó várható érték körüli ingadozását jellemző szám.
A valószínűségi változó várható érték körüli ingadozását jellemző szám.