Egy előző tanulmányomban meghatároztam a kézi lőfegyverekkel vívott tűzharc - ezen belül is a mesterlövészek tűzharca - lövész-lőfegyver-lövedék eszközrendszerétől (a továbbiakban: Rendszer) elvárható legfontosabb képesség követelmények közül a pontosság képességének számszerű követelményeit. Ugyanilyen fontos követelmény a hatásosság képességének a követelménye, amely azt mutatja meg, hogy a Rendszer milyen mértékben képes kiiktatni a további harcból a megcélzott objektumot. Magától értetődik, hogy ennek a képességnek csak akkor van értelme, ha a Rendszer máskülönben képes eltalálni a célt. A hatásosság képessége nem más, mint annak számszerűsíthető követelménye, hogy a lövedék képes-e a célobjektum harcképtelenné tételéhez szükséges - a célobjektum jellegétől függő mértékű - energiát közölni a célobjektummal. Egyszerűen fogalmazva, nem elég a célt eltalálni, azt olyan mértékben kell károsítani (energiával), hogy harcképtelenné is váljon. Ebből a követelményből adódik, hogy a szükséges energiamennyiség minden esetben az adott célobjektum fizikai jellemzőitől függ és teljesen más értékű fedetlen élőerő, vagy páncélozott objektum esetén. Mindenesetre a legfontosabb szabály, hogy ez a szükséges energiamennyiség kizárólag a célobjektumban értendő, ugyanakkor bizonyíthatóan valamilyen összefüggésben van a lövedék megindulási (közismert meghatározással: torkolati) energiájával. Minden fajta célobjektumhoz hozzárendelhető tehát egy minimálisan szükséges úgynevezett károsító-energia igény, amely energiamennyiséget a kívánatos eredmény elérése érdekében a lövedéknek a célobjektummal közölnie kell. Ezen értékek részletesebb meghatározására a későbbiekben visszatérek. Tanulmányom tárgya - a mesterlövész harca - szempontjából az energiák lehetséges fajtái közül elsősorban a lövedék célobjektumba csapódásakor képviselt mozgási energiája jöhet törvényesen számításba1. Első közelítésben feltételezve, hogy az energiaátadás 100% hatásfokkal megtörténik a célobjektumnak, a tényleges károsító-energia azonosnak vehető a lövedék becsapódási energiájával. Az általánosan használt mesterlövész fegyverek (puskák) mindegyikére jellemző, hogy a lövedékük a károsító-energiáját saját mozgási energiájából nyeri. A lövedék röppálya-menti pillanatnyi mozgási energiája pedig a lövedék torkolati energiájának mértékével van szoros összefüggésben. Tűzfegyverek alkalmazásakor a lőporban tárolt kémiai energia elégetéssel történő felszabadítása során keletkező gázok hőenergiájából nyert lövedék mozgási energia tekinthető a lövedék torkolati energiájának és ez az érték vagy gyárilag adott egy fegyver-töltény kölcsönhatásban, vagy a lövedék tömegéből és torkolati sebességéből számítható az:
közismert képlettel, ahol: E0 = a lövedék torkolati energiája [J] természetesen figyelembe véve, hogy a torkolati sebességre megadott mérési adat a fegyvercső torkolatától valamilyen nem túl távoli helyen (néhány méterre) mért értékkel azonos, mivel a tényleges torkolati sebesség csak nagyon bonyolult (és roppant drága) mérési elrendezéssel lehetne mérhető és nem is minden lövedékszerkezet esetében. Tekintettel arra, hogy az eltérés nem több néhány m/s-nál, a teljes pontosságra való törekvés nem is igazán indokolható. Léteznek közelítő számítások a valódi v0 meghatározására, mint például a néhány rögzített távolságban mért lövedéksebesség alapján a lövedék ballisztikai tényezőjének táblázatból2 való meghatározása, majd a v0 visszaszámítása . Ennél lényegesen egyszerűbb - de nem pontosabb - a NATO standard módszer, ahol a v0 értékét lineáris extrapolációval határozzák meg a 30 és 40 m távolságban mért lövedéksebességekből, a Ez az érték tekinthető a ballisztikus pályán repülő, póthajtás nélküli lövedék legnagyobb energiájának, azaz a célba-csapódáskor meglévő mozgási energia ennél csak kisebb lehet. Könnyen belátható tehát, hogy a lövedéknek a torkolati energiájából kell fedeznie az összes szükséges energiaigényét. Melyek ezek? Elsősorban a célobjektum leküzdéséhez mindenképpen szükséges károsító energia [EK], ami egyes esetekben azonos a lövedék becsapódási energiájával [EB], valamint az a szállító (transzportáló) energia [ETr], ami a károsító energia célba juttatásához szükséges. Az energiaegyenlet tehát a következő:
A képletből azonnal kiolvasható, hogy a transzportáló energia mennyiségével csökken a becsapódási energia mértéke a torkolati energiához képest. Az EK károsító energia-igény mértéke a célobjektumhoz kötődően viszonylag egyszerűen meghatározható. Fedetlen élőerő esetén, amikor a becsapódási és a károsító energia azonosnak tekinthető, azaz:
a szakmai konszenzus 40 - 240 J értékek között határozza3 meg a harcképtelenséghez elégséges energiamennyiség alsó határértékét. Nevezik ezt az értéket drámaiabban ölőhatárnak is. Én a továbbiakban a magasabb, EK=200 J értékkel kívánok számolni. Ha a célobjektum fedett (fedezék mögött tartózkodó, vagy kollektív, illetve személyi páncélzattal védett) élőerőnek tekinthető ez az érték magára az élőerőre nem változik, de figyelembe kell venni, hogy az elfedő-elem áttörése után a lövedéknek még mindig legalább ekkora energiával kell rendelkeznie, azaz a becsapódási energiának az EÁ átütési energiával magasabbnak kell lennie, mint a károsító energiának, azaz:
A lövedék becsapódási energiája könnyen számítható az [1] analógiájára:
képlettel, ahol: mlöv = a lövedék tömege [kg]; Az [5] képlet alapján kijelenthető, hogy a mesterlövésznek ismernie kell az általa használt lövedék sebességét az adott céltávolságban, mert ekkor könnyen számíthatja a lövedéke becsapódási energiáját és meghatározhatja, hogy az meghaladja-e a 200 J értéket. Természetesen a helyzet soha nem ilyen egyszerű. Az ölőhatár fogalmához hozzátartozik az a követelmény, hogy ezt az energiamennyiséget a lövedéknek maradéktalanul közölnie kell az élőerővel. Könnyen belátható, hogy, ha a lövedék áthatol a célobjektumon (és továbbrepül), akkor a károsító energia mértéke nem azonos a becsapódási energiával, hanem annál kisebb, azaz:
ahol az eddig használt jelöléseken túl: vbe = a lövedék becsapódási sebessége a célobjektumba [m/s]; A kérdés csupán az, hogy a [6] szerinti károsító energia mennyisége elegendő marad-e a célobjektum harcképtelenné tételéhez, azaz EK Képletbe foglalva:
ahol: Aco = a célobjektum teljes célozható felülete [cm2]; azaz az élőerő mesterlövész által támadható célfelületeinek összessége mindig sokkal kisebb, mint az élőerő-célobjektum teljes támadható felülete. A [7] képletbe foglalt törvényszerűséget figyelembe véve viszont kimondható, hogy csak az Ah célfelületeken elegendő a 200 J, mint minimálisan szükséges károsító energia mennyiséggel számolni. Ugyanez az analógia használható az esetek többségében a személyi páncélzattal védett élőerő mesterlövész által megvalósított támadásával kapcsolatban is, azaz a mesterlövész nem a páncélzattal fedett felületeket fogja alapesetben támadni, hanem a személyi páncélzat jellegéből adódóan fedetlenül hagyott, de halálos sérülés okozására is alkalmas felületeket. Mindkét esetben igaz tehát a [3] képlet, az eredményes találat valószínűsége a lőtávolság ismeretében (természetesen a lőtábla adatai alapján) meghatározható. A gyakorlatban azonban előfordulhatnak olyan szituációk, amikor - főleg a lövedékröppálya és a célobjektum egymáshoz képesti térbeli helyzete miatt - a cél csak a személyi páncélzaton keresztül támadható. Ekkor a [4] képletet kell alkalmazni, amihez viszont elengedhetetlen a személyi páncélzat átütéséhez szükséges EÁ energia mennyiségének ismerete. Jól felkészült mesterlövész azonban pontosan ismeri, hogy milyen távolságból támadhatók eredményesen az ellenség rohamsisakjai, védőmellényei és azok kiegészítő betétei. Minden részletezés igénye nélkül megállapítom, hogy pl.: vannak olyan kiegészítő védőmellénybetétek, amelyek még a 7.62 mm-es kaliberű, hagyományos szerkezetű páncéltörő puskalövedékekkel sem lőhetők át. Meggyőződésem azonban, hogy egy ilyen jellegű tanulmányban ennek a kérdésnek a részletes boncolgatása legalább is etikátlan lenne, és feleslegesen hozna veszélybe arra rá nem szolgált személyeket. Mindenesetre a mesterlövészek kiképzése során nem lényegtelen ezekkel a kérdésekkel kellő mélységben foglalkozni, illetve számszerűsítve oktatni, hogy egy adott lövedékfajta alkalmazása során egy adott testvédelmi páncél átütése mekkora EÁ energiát igényel. Kollektív páncélzattal, vagy műszaki akadályokkal védett élőerő eredményes támadhatósága - természetesen csak abban az esetben, ha a célobjektum elhelyezkedése a védelem mögött pontosan meghatározható - ugyanúgy a [4] képlettel számítható, mint a személyi páncélzat esetében is, de az EÁ mértékének meghatározása sokkal nehezebb, mint személyi páncélzatnál. Pontosan ismerni kell(ene) a lövedék áthatolási jellemzőit a szóban forgó anyagokon, amelyek a legtöbbször - éppen a gyártóművi adatok hiányában - csak kísérletekkel határozhatók meg. Homogén páncéllemezből képezett védelem esetén, amennyiben már legalább 1 lőtávolságban ismert a lövedék áthatolási képessége esetleg felhasználható a Jacob de Maar képlet4:
ahol: l = az átüthető páncéllemez vastagság [dm]; a [8] egyenlet K-ra való rendezésével kapjuk:
de a számítások elvégzéséhez már egy komolyabb képességű (legalább néhány lépésben programozható) zsebkalkulátor is szükségeltetik. A [9] egyenlettel a megadott páncélátütéshez tartozó lőtávolságon mért lövedék becsapódási sebesség, a lövedéktömeg és kaliber, valamint a páncélátütés mértékének ismeretében meghatározható a K páncélátütési tényező, amely ugyan lövedék és anyagfüggő, de a becsapódási sebességtől független jellemző. A számított értékek természetesen mindig merőleges lövedék-becsapódásra értendők! Ezt az értéket visszahelyettesítve a [8] egyenletbe jó közelítéssel meghatározható az átüthető páncélvastagság. Ugyanakkor figyelembe kell venni az eltérő páncélminőségeket. A szovjet-orosz töltények lövedékeinek (különböző hazai "Löfe" szabályzatokban megtalálható) páncélátütési adatai jól felhasználhatók a számításokhoz, mert a vizsgáló páncéljuk minősége jobb volt, mint a NATO minőségű nyugatiaké, tehát a gyengébb minőségű páncél biztos átütése garantálható. A 12.7x107 mm-es (orosz) B32 lövedék páncélátütési képességére az ismert adatok behelyettesítésével a [8] képletbe kaptam az 1. számú ábrát:
1. számú ábra: a 12.7 mm-es B32 lövedék páncélátütő képessége a céltávolság függvényében Az ábra alsó görbéje a lövedék műszaki dokumentációjában megadott adatok alapján számított értékeket mutatja, a felső görbe értékei saját méréseim adatainak felhasználásával végzett számításaimból származnak. Az az általános tapasztalat, hogy ha a lövedék teljes kaliberben átütötte a páncéllemezt, akkor a lemez mögött a mozgási energiája még bőven meghaladja az ölőhatárt, ugyanakkor szabálytalanul kóvályogni fog és erős repeszhatást is produkál mind a lemezből, mind saját magából. Ebben az esetben tehát elégséges feltétel a páncél átütése. Az eddig felsoroltak alapján a lövedék becsapódási energia igénye a [4] és [5] képletekkel már minden esetben számszerűen meghatározható. Egyes azonos kaliberű lövedékfajták gyors összehasonlításához szívesen használom az Egerszegi János úr, a Magyar Ballisztikai Társaság alelnöke által alkotott lövedék
Minél kisebb az A kérdés ezután az, hogy a szükséges mértékű becsapódási energiához milyen mértékű torkolati energiával kell ellátni a lövedéket. Ha a [2]-be behelyettesítjük a [4]-et kapjuk:
amely képletben még az ETr transzportáló energia mértéke nincs meghatározva. A transzportáló energia nagyságáról (az energiaigényről) kijelenthető, hogy az egyrészt a lövedék geometriai kialakításától és műszaki jellemzőitől, másrészt annak a közegnek a pillanatnyi és térbeni állapotától függ, amelyben a lövedék a röppályáját bejárja. Egy adott műszaki kialakítású lövedék röppálya menti lassulását a lövedék és az azt körbevevő közeg kölcsönhatása határozza meg. Általános (és mindennapi) esetben - amikor a lövedék adott állapotú levegőben járja be a röppályáját - a lövedékhez hozzárendelt számított, vagy kimért lőtáblázatok adatseregének vonatkozó adataiból lehet az adott lőtávolsághoz tartozó EB becsapódási energia értékét kiemelni (vagy a becsapódási sebességből kiszámítani). a [2] átrendezésével kapjuk, hogy:
ami azt jelenti, hogy a transzportáló energia hagyományos tűzfegyver lövedéke esetében a lövedék torkolati és becsapódási energiájának a különbsége. Miután ezek az adatok - amint már többször megállapítottam - az adott lövedék (egész pontosan a fegyver és lövedék részrendszer) külballisztikáját leíró lőtábla alapadatai a mesterlövésznek (a Rendszer harmadik elemének) nincs más feladata, mint megállapítani, hogy az adott céltávolságban a lövedék becsapódási energiája meghaladja-e a [3], vagy [4] képlet szerinti energiaszükségletet. Ha az adott lőtávolsághoz tartozó becsapódási energia ennél az értéknél kisebb, akkor nem érdemes erről a lőtávolságról eredményt remélve célzott lövést megkísérelni, mert a fegyver-lövedék rendszer torkolati energiája eleve kevesebb a szükségesnél, bár néhány esetben nem kizárt más külballisztikai jellemzőkkel bíró lövedék alkalmazása. Egy adott kaliberben (pl.: 7,62x54R, vagy 7.62x51 NATO, vagy 7.62x63 Springfield [30-06 Spr.], stb.) a töltényeket általában többféle lövedékkel is szerelik, a könnyűlövedékektől a nehézlövedékekig. Egy adott konstrukciójú lövedék röppálya-menti mozgási energia veszteségét az adott kivitelre érvényes ballisztikai tényező (más megközelítésben ballisztikai együttható) értéke szabja meg. A mozgási energia veszteségre (ami egyenlő a transzportálási energiával) felírható, hogy:
tehát a lövedék kezdő és becsapódási sebessége négyzeteinek különbségével egyenesen arányos, így a lövedék lassulásának a függvénye. Végül is az adott célobjektum leküzdéséhez, ha az fedetlen élőerő, elegendő 200 J becsapódási energia, azaz az energiaegyenlet felírható:
és mivel a [13] képletben a vct lövedék becsapódási sebesség értéke a kérdéses, arra átrendezve és egyszerűsítve:
azaz elegendő, ha a lövész ismeri az általa éppen használt lövedék kg-ban számított tömege gyökének az értékét (ami egy könnyen megjegyezhető állandó adat), abból rögtön következik a szükséges minimális lövedéksebesség is a célban. Például a 7.62 mm-es 11.2 g-os 39M D nehézlövedék esetén ez 189 m/s, 9.7 g-os LPSz lövedék esetén már 203 m/s, vagy 12.7 mm-es B32 lövedék esetén csupán 91 m/s. Kérdés marad azonban, hogy ezek a lövedék sebességek milyen lőtávolságokhoz tartoznak, azaz milyen távolságon belül lehet a biztosan hatásos találatra számítani? A legegyszerűbb esetben a mesterlövésznek rendelkezésre áll a fegyver-lövedék részrendszer legalább olyan részletes lőtáblázata, amely a lőtávolságokhoz tartozó lövedéksebességeket is megadja. Mivel ezek a lőtáblázatok általában 100 m-es (vagy 100 yardos) lépésenként adják meg az adatokat, a legcélszerűbb a szükséges sebességhez legközelebbi nagyobb sebességhez tartozó lőtávolságot felső korlátnak figyelembe venni (az EB biztosan nagyobb lesz, mint a szükséges EK). Lőtáblázat hiányában a feladat a terepen megoldhatatlan. A feladatra való előkészületek során ("tantermi körülmények között") viszont néhány számítás elvégezhető. A röppálya-menti sebességvesztés ütemére a már említett ballisztikai tényező ad útmutatást. Ugyanakkor mérésekkel az is bizonyítható, hogy ez a jellemző erősen függ a lövedék pillanatnyi sebességétől (még akkor is, ha annak a levegőrétegnek, amelyben a lövedék halad, a jellemzői konstansnak értékelhetők), tehát nem tekinthető abszolút állandónak. A ballisztikai tényező kiszámítására használatos a következő képlet:
vagy egy adott lövedékre egyszerűsítve (d löv és m löv állandó):
Ahol az eddig használt jelöléseken kívül: c = a ballisztikai tényező Továbbá az i meghatározásához használható pl.: 12.7 mm-es B32 lövedék alkalmazása esetén (nagykaliberű mesterlövészek előnyben!) dr. Piroska György úr, a Magyar Ballisztikai Társaság elnöke által meghatározott harmadfokú polinom6:
ahol: L = lőtávolság [m] Egy adott lövedék c ballisztikai tényezőjének a 2. számú ábrán (amely a 12.7 mm-es B32 lövedék alaplőtáblájából7 vett lövedéksebesség adatokkal a GAU táblás saját számításaim alapján meghatározott ballisztikai tényezőket tartalmazza) látható mértékű változása, illetve az idézett polinom alapján érzékelhető, hogy az i értéke erősen lőtávolságfüggő és csak adott lőtávolságokhoz tartozóan tekinthető állandónak, amint azt a dr. Piroska-féle polinom is bizonyítja.
A 2. számú ábra bal oldali diagramjában szereplő folyamatos vonallal jelölt c ballisztikai tényező értékek mindig csak két, 100 m különbségű (pl.: 200-300 m) röppálya szeletben érvényesek, míg a pontozott, a dr. Piroska-féle polinommal számított görbe c értékei az adott lőtávolságig meghatározott átlagértékeknek tekinthetők. A számítható, vagy rendelkezésre álló c ballisztikai tényező érték és a lövedék v 0 torkolati sebesség és a v ct ismeretében meghatározható a v ct-hez tartozó lőtávolsága is következő képlet felhasználásával:
ahol: x = a céltávolság [m]; D(v0) és D(vx) = az aktuális távolságon igaz lövedéksebességhez tartozó Siacchi-függvények numerikus megoldásának értékei. A vct = vx helyettesítéssel a [17] megoldható x-re:
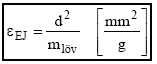
amely eredmény már a keresett lőtávolságot adja. A számítási eljárásnak csak annyi árnyoldala van, hogy a Siacchi függvények numerikus megoldásait tartalmazó táblázatok (pl.: a GAU-tábla) a legritkább esetben (gyakorlatilag sohasem) állnak a mesterlövész rendelkezésére, tehát esélye sincs arra, hogy ezeket a számításokat képes legyen elvégezni. A nemzetközi szakmai gyakorlat azonban már érezhetően túllépett ezen a problémán, mert a - főleg a Rendszer pontosság-képesség biztosításának elengedhetetlen feltételét jelentő - katonai kivitelű zsebszámítógépek (pantopok) egyes nálunk sanyarúbb sorsú NATO társak katonai (és rendvédelmi) mesterlövészei számára biztosítottak (általában egy közvetlen csatlakoztatású kézi meteorológiai mérőműszerrel együtt). Tekintettel arra azonban, hogy a külballisztikai jellemzők alapértékektől való eltérésének kevésbé drámai a befolyása a hatásosság-képességre, mint a pontosságra egy adott lövedékhez tartozó alap lőtáblázat birtoklása és használata már lényegesen előnyösebb helyzetbe juttat. Ebből a vct sebességhez tartozó céltávolság könnyen kiolvasható. Az épp alkalmazott lövedékünk hatásosság-képességének gyors megítélésére használhatjuk a keresztmetszeti terhelés jellemzőt, amely nem más, mint a lövedék tömegének [mlöv] és keresztmetszetének [Alöv] a hányadosa:
erről a viszonyszámról mindössze annyit érdemes megjegyezni, hogy minél magasabb az értéke, annál kevesebb lesz a lövedék ETr transzportáló energia igénye, magyarul annál kisebb mértékben fog a röppályán a lövedék lassulni, mozgási energiát veszíteni. Sajnos ez az eltérés azonban egyszerű lineáris arányossággal nem írható le. Felhasználható azonban egy ismert és lőtáblázattal rendelkező lövedék hatásosság-képességével való összevetésre és igen durva becslésre. Egyes újabb források egyszerűbb változatát alkalmazzák a [19] képletnek, a
ahol: dlöv = a lövedék kalibere mm-ben, figyelembe kell venni azonban, hogy a két eltérő
és a hagyományos szerkezetű lövedékek külballisztikai viselkedésének összehasonlításán túl a célban kifejtett hatások jó összehasonlításul is szolgál. A [19] és [19a] képletek értelmében adott kaliberben általában a lövedéktömeg növelésével lehet az
3. számú ábra: 12.7 mm-es lövedékek összehasonlítása
Mindezek alapján, bár nem zárható ki az alap lőtáblázat adatoktól kedvezően eltérő transzportáló energia igényű lövedék alkalmazása, nagyobb a valószínűsége annak, hogy a mesterlövész az alap lőtáblázat adataiból határozza meg a célobjektumhoz rendelhető optimális lőtávolságot. A lövedék viselkedése a normálistól8 jelentősen eltérő, vagy rétegesen változó légállapotok esetén, alapvetően a pontosság képességét befolyásolja, de nem zárható ki jelentős transzportáló energiaigény növekedés sem. Emiatt a mesterlövész számára elengedhetetlen olyan lőtáblázat használata, amely az ilyen esetekben érvényes helyesbítéseket, vagy azok gyors meghatározását elősegítő számítási módszereket is tartalmazza. Kijelenthető tehát, hogy a mesterlövész a saját mesterlövész puskája és tölténye (lövedéke) - mint részrendszer - egymáshoz rendelésével elkészített lőtáblázata alapján, valamint az általa teljesen felmért célobjektum jellemzők (amibe beletartozik a cél távolságának, védettségének, stb. meghatározása) ismeretében eldönti, hogy az adott lőtávolságból egyáltalán lehetséges-e egy hatásos (azaz a Rendszer hatásosság-képességének megfelelő) lövés leadása. A mesterlövésznek tehát meg kell megvizsgálnia, hogy az adott lőtávolságon a lövedék becsapódási energiája egyszerű esetben meghaladja-e a 200 J, fedett cél esetében az EÁ+200 Joule értékeket. Amennyiben a válasz nemleges, vagy kétséges, akkor vagy megvárja, hogy a cél közeledjen tüzelőállásához, vagy ő közelíti meg a célt a hatásosság-képesség szerinti lőtávolságon belüli távolságra. Nem élőerő elleni harc esetén természetesen nem a 200 J, hanem az adott célobjektum megsemmisítéséhez szükséges EK energiaszükséglettel kell számolni. Összefoglalva az eddigieket megállapítom, hogy egy mesterlövésznek bírnia kell fegyvere és annak lövedéke olyan külballisztikai adatainak pontos ismeretét, amelyekből a lövedék röppálya menti (a cél távolságához köthető) mozgási energia értékeit meg tudja határozni, és a célobjektumot csak abban az esetben szabad megtámadnia, amennyiben a lövedék becsapódási energiája biztosítja annak harcképtelenné tételét. Ennek hiányában a célobjektum képes lehet:
illetve a célobjektumot esetleg védő szervezet biztosan képes lesz aktív ellentevékenységre és a cél kivonására a támadható háromdimenziós térrészből. A felsorolt esetekben a mesterlövész egyrészt nem hajtja végre a feladatát és ezzel magát, és oltalmazandó társait hozza veszélybe, másrészt nagyobb óvatosságra ösztönözve a célobjektumot a feladat sikeres újbóli megkísérlésének az esélyeit jelentősen rontja, vagy lehetetlenné teszi.
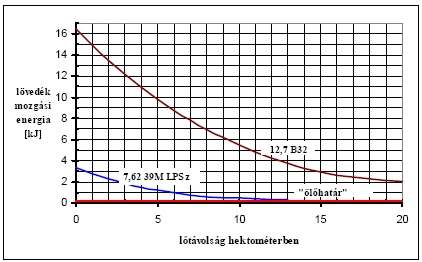
Az egyes, a mesterlövészek szokásos kalibersávjába (7.62 - 12.7 mm ) tartozó lövedékek (töltények) lőtáblázatait tanulmányozva megállapítható továbbá, hogy fedetlen élőerő elleni harc esetén a mesterlövész lőtávolságát nem a hatásosság, hanem a pontosság képessége fogja meghatározni. Mint ahogy a 4. ábrán látható, ezekben a kaliberekben az ölőhatár energiamennyiségi-követelményt jelentő 200 J a lőtáblázatok szerinti teljes lőtávolságokon rendelkezésre áll, míg a pontosság képesség szerinti maximális lőtávolság mindig jóval kevesebb, mint a lőtábla szerinti maximális. A hatásosság képessége - mint ahogy az az eddigiekből is belátható, nem tekinthető a Rendszer saját képességének, hanem csak a fegyver-lövedék részrendszerének, mert a mesterlövész, mint a Rendszer humán eleme ezt a képességet csak a lehetőségek hibás felmérésével tudja befolyásolni, a lövésfolyamat (a Rendszer tényleges működése) közben - amennyiben a pontosság képessége máskülönben megvalósul - azonban már nem. Azt a képességet viszont, hogy a mesterlövész saját részrendszere hatásosságát az adott célobjektumra minden esetben megfelelő pontossággal tudja megítélni csak igen magas színvonalú kiképzéssel, a részrendszer műszaki jellemzőinek pontos megismertetésével, valamint a célobjektum jellemzőinek megfelelő szintű felismerésének oktatásával és gyakoroltatásával lehet kifejleszteni. Ennek elmulasztása végső soron a mesterlövész alkalmazását teszi értelmetlenné. Amennyiben az MH belátja, hogy mesterlövész katonát (szakembert) nem lehet SzVD távcsöves puskára építve kiképezni és alkalmazni, és végre valódi mesterlövész puskákkal látja el az érintett állományt, akkor azt is be kell egyidejűleg látnia, hogy a drága fegyver mit sem ér a célnak megfelelően kimagasló (általában match) minőségű töltények és a szükséges hordozható (zsebben elférő) számítástechnikai háttér biztosítása nélkül. A lőtávolság pontos (legalább ±10 m-en belüli) meghatározása mind a pontosság, mind a hatásosság szempontjából elengedhetetlen. A modern katonai mesterlövész feladatokban egyre inkább tért nyer a nagytávolságú pontos és hatásos lövés képességének a követelménye, nekünk fel kell nőni ehhez a feladathoz, aminek a műszaki kérdéseit egy másik tanulmányban tervezem kifejteni.
Felhasznált irodalom: Híhalmi Harmos Zoltán: Tüzérlövéstan; Magyar Királyi Honvédelmi Minisztérium kiadása Budapest, 1937. Karl G. Seiller-Beat P Kneubuehl: Wound Ballistics (angolra fordította: Ruth Rufer és Jack Hawley) Elsevier Science B.V., Asterdam 1994. Textbook of Military Medicine (főszerkesztő: colonel Russ Zajtchuk, MC, U.S. Army, Conventional Warfare) - Ballistic, Blast, and Burn Injury (speciality editors Ronald Bellamy - Russ Zajchuk); Walter Reed Army Medical Center Walter Reed Army Institute of Researc, Wasington D.C. (évszám nélkül) www.fcsa.co.uk/reloading_data2.htm Ábrák: 1. számú ábra: a 12.7 mm-es B32 lövedék páncélátütő képessége a céltávolság függvényében (saját grafika) 2. számú ábra: a 12.7 mm-es B32 lövedék ballisztikai tényezőjének változása a röppályán (saját grafika) 3. számú ábra: 12.7 mm-es lövedékek összehasonlítása (a baloldali fotó saját, a jobb oldali forrása: www.hornady.com) 4. számú ábra: a lövedékek mozgási energiájának változása a röppályán (saját grafika) 1 a feleslegesen szenvedést okozó lövedékek - köztük a robbanótöltetet hordozók - alkalmazását a nemzetközi szerződések tiltják, bár attól még (főleg a 12.7 mm-es kaliberben) léteznek. 3 Karl G. Seiller-Beat P Kneubuehl: Wound Ballistics (angolra fordította: Ruth Rufer és Jack Hawley) Elsevier Science B.V. Asterdam 1994. 303. old.; ahol a 40 J a francia, a 240 J a szovjet katona harcképtelenné tételéhez szükséges saját maguk megadta határérték. Az átlagos angolszász érték csupán 80 J. Mint reális felső értéket vettem a 200 J-t tekintetbe (saját megjegyzésem) 4 Közli: Híhalmi Harmos Zoltán: Tüzérlövéstan 394. oldalán; Magyar Királyi Honvédelmi Minisztérium kiadása Budapest, 1937. A közölt jelölések és dimenziók eredeti szöveg szerintiek. 5 ebben az esetben a mm 2/g és a m 2/kg azonos numerikus értéket ad 6 Dr. Piroska György úr szóbeli engedélyével közlöm 8 Normál állapotúnak tekinthető az ICAO előírás szerint a 288 K hőmérsékletű, 0.10135 MPa nyomású, 1,205 g/m 3 sűrűségű, 0% relatív páratartalmú levegő közeg. |

 [1]
[1] [5]
[5]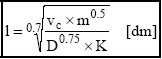 [8]
[8] 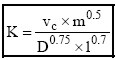 [9]
[9] 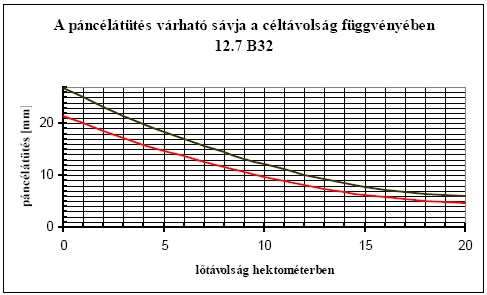
 [10]
[10] 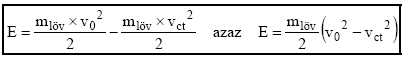 [13]
[13] 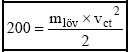 [14]
[14] 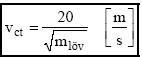 [15]
[15] 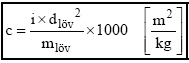 [16]
[16]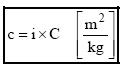 [16a]
[16a]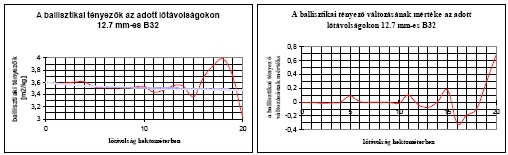
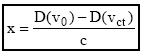 [18]
[18]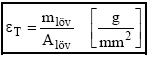 [19]
[19]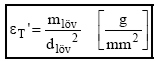 [19a]
[19a] 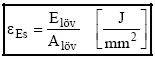 [19b]
[19b]