Absztrakt A repülőgépek fedélzetén végrehajtott mérések döntő része közvetett mérés. A cikkben a szerzők bemutatják, hogy a matematikából ismert becslés művelete hogyan alkalmazható a repülőgépek fedélzeti rendszereiben erre a mérési módszerre. A becslési feladatot a szerzők a legkisebb négyzetek módszerével oldják meg azokra az esetekre, amikor a mért és a meghatározni kívánt jellemzők közötti függvénykapcsolat nem pontosan ismert, illetve ha figyelembe vesszük a véletlen mérési hibákat és az egyes mérések eltérő mérési pontosságát. Most measurements on board of aircraft are indirect ones. In the article authors apply mathematical operation of estimation for these measurements onboard. The task of estimation authors solve using method of minimal quadrates in cases when the relation between measured and wanted characteristics is not known exactly or rather the random faults of measurements and the different precision of each measurement are considered. Kulcsszavak: repüléstechnika, repülésszabályozás, becslés művelete
A repülőgépek fedélzeti rendszereiben (pl. az adatrögzítő rendszerekben, a fedélzeti beépített önellenőrző rendszerekben, automatikus repülésszabályozó rendszerekben, stb.) sok esetben szükséges lehet ismeretlen jellemzők összességének meghatározására olyan mérések eredményei alapján, amelyek általában hibákat tartalmaznak. Az ismeretlen jellemzők így meghatározott értékeit becsült értéknek vagy becslésnek, a becslés meghatározott folyamatát, pedig becslési feladatnak nevezzük. Általánosan elmondhatjuk, hogy a becslési feladat megoldása - vagyis a becsült értékek meghatározása - a mérési eredmények és adatok feldolgozásának egyik formája [1]. Ebben az esetben tehát az érzékelés helye és az adatfelhasználás helye közé olyan elemet iktatunk, amely a becslési feladatot végrehajtja. A meghatározni kívánt ismeretlen jellemzők összességét jelöljük X1, X2, ., Xn. Ezek meghatározni kívánt becsült értékei x1, x2, ., xn. A közvetett mérés lényegéből következik, hogy nem közvetlenül X1, X2, ., Xn értékeit mérjük, hanem az azokkal meghatározott és ismert függvénykapcsolatban lévő y1, y2, ., yk jellemzőket. Tehát:
A továbbiakban azt a legegyszerűbb esetet vizsgáljuk, amikor a mért jellemzők az ismeretlen jellemzőkkel lineáris függvénykapcsolatban vannak, vagyis az (1) egyenlet az alábbi formában írható fel:
ahol hij - ismert együtthatók. A (2) k lineáris algebrai egyenletből álló n ismeretlenes egyenletrendszerben az ismeretlenek Xj, Az, hogy az egyenletrendszernek nincs pontos megoldása, fizikailag a következő okokra vezethető vissza [1]:
Akkor az ismeretlen értékek becslésének feladatát vizsgálhatjuk úgy, mint a (2) egyenletrendszer közelítő megoldásainak meghatározását, azzal a feltételezéssel, hogy yi, Az összes lehetséges közelítő megoldás közül célszerű a valamilyen - általunk előzetesen meghatározott - értelemben legjobb megoldás kiválasztása. Az ilyen megoldás megkeresésének egyik lehetősége a legkisebb négyzetek módszerének alkalmazása. A módszerrészletes leírása, bemutatása a [2], [3] és [4] irodalmakban megtalálható. A módszeren belül megkülönböztetünk determinisztikus és statisztikus megközelítést. A determinisztikus megközelítést akkor alkalmazzuk, ha véletlen mérési hibák nincsenek, vagy az ilyen hibák statisztikai jellemzőit nem ismerjük. A statisztikus megközelítésben a véletlen hibák statisztikai jellemzőit ismerteknek tételezzük fel. Az adatfeldolgozás során használt matematikai apparátus ilyenkor lehetővé teszi a mérések eltérő pontosságának a figyelembe vételét is [1]. A (2) egyenletrendszernek a legkisebb négyzetek módszerével meghatározott megoldásait - vagyis a becsült értékeket - az előzőeknek megfelelően jelöljük mint
Belátható, hogy minél kisebbek bi értékei, annál jobbak a becsült értékek, vagyis xi értékek annál jobban közelítik a valós Xi értékeket. Legyen ezért a közelítő megoldás minőségi jellemzője a bi "egyeztetlenségi" értékek függvénye:
A legkisebb négyzetek módszerében olyan négyzetes minőségi jellemzőt használunk, amely a bi értékek négyzetösszege [1]:
A (3) egyenletrendszer optimális megoldása a legkisebb négyzetek módszerével olyan xj,
Ebből a kritériumból ered a módszer elnevezése is. Mivel a J1 függvényt minimalizálni kell, így azt költségfüggvénynek is tekinthetjük [2], [3]. Mivel a J1 minőségi jellemző xj,
és
Bizonyítható [4], hogy a (7) n egyenletből álló n ismeretlenes egyenletrendszer együtthatóival felírt determináns nem zérus értékű, tehát a (6) egyenletrendszer x1, x2,., xn változókra egyetlen megoldást ad. A (7) egyenlet megoldása lesz az eredeti (2) egyenletrendszer megoldása a legkisebb négyzetek módszerével, determinisztikus megközelítésben. Statisztikus megközelítésben szintén a (2) egyenletrendszerből indulunk ki, de most feltételezzük, hogy az rendelkezik zérustól eltérő értékű egyértelmű megoldással. A problémát most az okozza, hogy yi értékeit mérési hibával határozzuk meg, vagyis a mérések eredményei nem yi, hanem azoktól eltérő, de értékekben közeli jellemzők:
ahol vi - véletlen mérési hibák, amelyek megjelenésének következtében zi szintén véletlen értékű lesz. Akkor a (2) egyenletrendszert most így írhatjuk fel:
Ennek az egyenletrendszernek nincs pontos, egyértelmű megoldása. Ha zi véletlen értékek statisztikai jellemzőit nem ismerjük, akkor az egyenletrendszer zi értékeire megoldható determinisztikus megközelítésben. Ha ezek a jellemzők ismertek, akkor célszerű a statisztikus megközelítést alkalmazni. Így olyan pontosabb megoldást kapunk, amely figyelembe veszi a mérések eltérő pontosságát is [1]. Legyen vi véletlen mérési hibák várható értéke zérus: M[vi] = 0, Fogadjuk el továbbá, hogy a véletlen értékek normál eloszlásúak:
Ennek megfelelően a zi véletlen értékekre is felírhatjuk:
Az xj becsült értékek meghatározásához a (2) egyenleteket felhasználva helyettesítsük az
Legyen valamely Ai véletlen esemény zi véletlen értékeknek a
Legyen továbbá A véletlen esemény valamennyi zi értéknek a fenti intervallumba esése, vagyis A=A1A2.Ak. Az elfogadott kikötések értelmében zi véletlen értékek egymástól függetlenek, ezért Ai események szintén egymástól függetlenek lesznek. Akkor:
ahol Ha
ami lehetővé teszi x1, x2, . xn becsült értékek meghatározásában a maximum-likelihood módszer alkalmazását [2] [3]. Ennek értelmében tegyük fel, hogy P[A]=max, vagyis A esemény bekövetkeztének valószínűsége maximális. Ez a követelmény akkor teljesül, ha X1=x1, X2=x2, ., Xn=xn, amely esetben biztosítva lesz a (12) függvény maximuma, amely a hatványkitevőben lévő kifejezés abszolút értékének minimuma esetén következik be. Ebből a (9) egyenletrendszer x1, x2, .xn megoldásainak optimumkritériuma felírható:
A kritériumból következő egyenletrendszer:
A parciális deriváltakat meghatározva:
Ezt a kifejezést j=1, 2, ., n értékekre sorban egyenlővé téve zérussal és rendezve a következő egyenletrendszert kapjuk:
A fenti egyenletrendszer megoldása adja a (9) egyenletrendszer megoldását a legkisebb négyzetek módszerével, determinisztikus megközelítésben. A (13), (15) kritériumokat és a (7), (15) egyenleteket összehasonlítva láthatjuk, hogy statisztikus megközelítésben az yi értékek eltérő mérési pontosságát a mérési hibák szórásnégyzetével vesszük figyelembe. Azonos pontosságú méréseknél ezek a szórásnégyzetek egymással megegyeznek és a (13), (15) egyenletek megegyeznek az (5), (7) egyenletekkel. A (15) egyenleteket értelmezhetjük mint a z1, z2, ., zk mért értékek és az x1, x2, ., xn becsült jellemzők közötti lineáris kapcsolatrendszert. Mivel a z mért értékek véletlenek, így az x becsült értékek is véletlenek lesznek. Ezek statisztikai jellemzői a következők [1]:
A gyakorlatban sokszor nem a fő X1, X2, ., Xn jellemzőket kell becsülnünk, hanem azok lineáris függvényét: S=a1X1 + a2X2 + . +anXn. (16) Ezt a függvényt lineáris alaknak, S értékének becslését pedig a fő paraméter lineáris alakja becslésének hívjuk. Az S jellemző optimális becslése ebben az esetben: s=a1x1 + a2x2 + . + anxn, ahol x1, x2, . xn - X1, X2, ., Xn értékeknek a legkisebb négyzetek módszerével meghatározott optimális becslései. Az s becslés optimális volta abban áll, hogy az torzítatlan, hibája pedig minimális szórásnégyzettel rendelkezik, vagyis M[s] = S és D[s - S] = min. Korszerű repülőgépek fedélzeti rendszereiben a becslés fentebb meghatározott algoritmusa a fedélzeti számítógépben kerül végrehajtásra. A központi mikroprocesszor műveleti sebessége olyan, hogy az biztosítja a felhasználók megfelelő kiszolgálását.
FELHASZNÁLT IRODALOM [1] Taraszov, V. G.: Obrabotka informacii v avtomatyizírovannih szisztyémah upravlényija (VVIA im. Prof. N. E. Zsukovszkovo, Moszkva, 1974) [2] Granino A. Korn - Theresa M. Korn: Matematikai kézikönyv műszakiaknak (Műszaki Könyvkiadó, Bp., 1975) [3] I. N. Bronstein - K. A. Szemengyajev: Matematikai zsebkönyv (Műszaki Könyvkiadó, Bp., 1987) [4] Edwin F. Beckenbach: Modern matematika mérnököknek (Műszaki Könyvkiadó, Bp., 1965) |

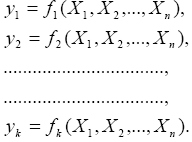 (1)
(1) 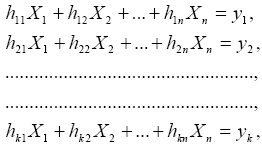 (2)
(2) 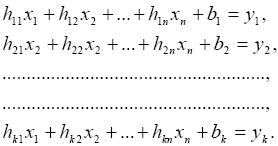 (3)
(3) 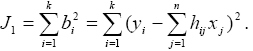 (4)
(4) 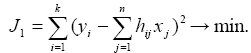 (5)
(5) 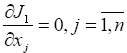 . Ezen egyenletek alapján határozhatjuk meg a keresett x j becsült értékeket. A parciális deriváltakat kifejtve
. Ezen egyenletek alapján határozhatjuk meg a keresett x j becsült értékeket. A parciális deriváltakat kifejtve 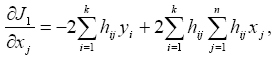 (6)
(6) 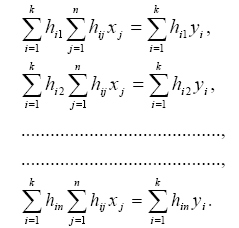 (7)
(7) 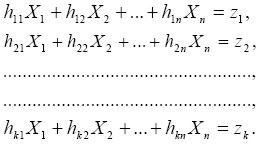 (9)
(9) 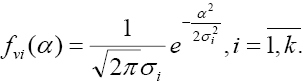
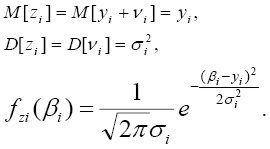 (10)
(10) 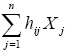 :
: 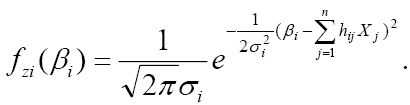
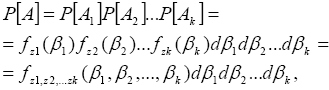 (11)
(11) 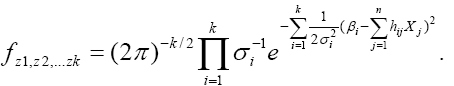
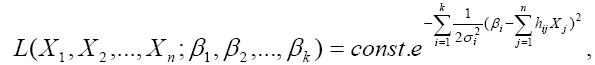 (12)
(12) 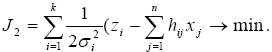 (13)
(13) 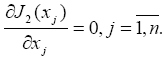 (14)
(14) 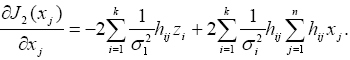
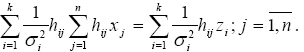 (15)
(15)