ROBOTHADVISELÉS 7. TUDOMÁNYOS SZAKMAI KONFERENCIA
2007. november 27.
KÜLÖNSZÁM |
![]() Neszveda József:
Neszveda József:
IDŐSZAKOSAN HASZNÁLT HARCTÉRI ESZKÖZÖK MEGBÍZHATÓSÁGI SZINTJÉNEK
ELEMZÉSE DISZKRÉT-DISZKRÉT MARKOV MODELLEL
Absztrakt Az időszakosan működtetett, energiamentesen tárolt technológia definiálása. Az 1002D irányítási struktúra választásának indoklása. Az 1002D irányítási struktúra Markov modelljének elemzése diszkrét időpontokban. Az IEC 61508 szabvány fogalmainak illesztése az időszakosan működtetett, energiamentesen tárolt technológiákra. A SIL (megbízhatóság sérthetetlenség szint) meghatározás képletei. Definition of the periodically operated and durative stored without power technologies. Justification of choice of the 1002D structure. Analysis of the Markov model of the 1002D structure at discrete time. Application of the terms of the IEC 61508 standard on the periodically operated and durative stored without power technologies. Equitation of assay of the SIL. Kulcsszavak: redundáns struktúra, Markov modell ~ redundant structure, Markov model Bevezetés Vannak olyan technológiák, melyek csak néhány napon keresztül üzemelnek egy évben, vagy csak egyszer kerülnek bevetésre. A két működtetés között vagy a működtetést megelőzően huzamosabb ideig, esetleg évekig energia mentesített állapotban raktározták őket. Ugyanakkor az üzemelés időszakában folytonos üzemmódban, rendkívül megbízhatóan kell működniük. Az elektronikus hadviselés számos ilyen technológiát használ. A harctéri felderítő eszközök, a mobilrobotok, a légvédelmi rakéták ráemelő és kilövő eszközei alkalmazásakor különösen fontos kérdés, hogy mekkora a valószínűsége annak, hogy amikor szükséges, akkor az eszköz ténylegesen működni fog? Azért, hogy a működés megbízhatóságára a szakhatóságok számára ellenőrizhető választ lehessen adni kidolgozták az IEC 61508 szabványt [1], ami definiálja az alapfogalmakat és bevezeti a biztonság sérthetetlenség szint (SIL) mérőszámot. A definíciók közül a téma szempontjából fontosakat, valamint a SIL mérőszám értelmezését eszközökre, és ezen eszközökből épített redundáns rendszerekre az előző cikkemben [2] már tárgyaltam. Az időszakosan működtetett, energiamentesen tárolt eszközök, technológiák három jellegzetesen eltérő üzemállapottal rendelkeznek. Ezek a folytonos, az időszakos teszt, és az energiamentesen tárolt üzemmód. A folytonos üzemmód sajátossága, hogy viszonylag rövid (5 - 10 nap). Az időszakos teszt üzemmód célja és hatása a megbízhatóságra ugyanaz, mint a redundáns folytonos technológiákban a kezelhető hiba detektálása, és javítása. Az energiamentesen tárolt állapotban az eszköz nem működik, és így biztosan nem detektálható hiba, de a tapasztalatok szerint az első működtetéskor ugyanolyan valószínűséggel hibásodik meg, mint amikor az eszköz tápellátása biztosított, de fizikailag nem működtetett. Az időszakosan működtetett eszközök, a végrehajtott műveletek gyakoriságát tekintve, a vész, védelmi rendszerekkel mutatnak hasonlóságot. Normál esetben a folytonos technológiák vész, védelmi rendszere évekig nem működik, ezért az esetükben is az a kérdés, hogy mekkora a valószínűsége annak, hogy amikor szükséges, akkor az eszköz ténylegesen működni fog? A vész, védelmi rendszereket az IEC61508 szabvány az alacsony működés igényű üzemmódban működő eszközök, vagy technológiák közé sorolja. Az 1. táblázat az alacsony működés igényű üzemmód (SIL) értékeihez tartozó λ [1/év] értéktartományokat tartalmazza. A működés gyakorisága alapján az időszakosan működtetett, energiamentesen tárolt eszközök megbízhatósága ugyanezzel a biztonság sérthetetlenség szint (SIL) mérőszámmal jellemezhető.
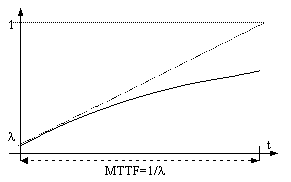
Bármely berendezés, technológia R(t) megbízhatósága az üzemelési idő függvényében az 1-λ értékről folyamatosan csökken, ahol a λ hibaarány az MTTF (Mean Time To Failure - átlagos idő a meghibásodásig) reciprok értéke. Értelemszerű, hogy a meghibásodás valószínűsége P(t)=1-R(t) a működési idővel arányosan, nő. A tárolt berendezések P(t) meghibásodási valószínűsége az időfüggvényében legalább úgy növekszik, mint a folyamatosan használtaké, vagyis az energiamentes állapot a meghibásodás valószínűségének növekedésében nem okozz különbséget. Üzembeállításkor egy berendezés vagy technológia meghibásodásának kezdeti valószínűsége λ értékről indul.
A vizsgált eszköz csoport átlagos paraméterei A harctéri felderítő eszközök, a mobilrobotok, a légvédelmi rakéták ráemelő és kilövő eszközeinek irányító rendszerei jellemzően 1 bemeneti (12 - 16 DI), 1 kimeneti (4 - 8 DO), és 1 adó és/vagy vevő (RF kommunikációs) modullal rendelkeznek. • MTTF = 500 [év] ( • A kielégítő megbízhatóság érdekében redundáns irányítási rendszert kell alkalmazni. Az 1002D struktúra választásának indoklása Általánosan elterjedt vélemény, hogy a redundancia növeli a megbízhatóságot. Ez azonban nem ilyen egyértelmű. A 2002 struktúra a kezelhető hibákra javítja, de a veszélyes hibákra rontja a megbízhatóságot, viszont az 1002 struktúra a kezelhető hibákra rontja, de a veszélyes hibákra javítja a megbízhatóságot. A 2. táblázatban a kontaktusok a redundáns ágak hibaarányát (λ A , λ B ) ábrázolják, és nincs közük [2] az irányító berendezés kimeneti kontaktusaihoz.
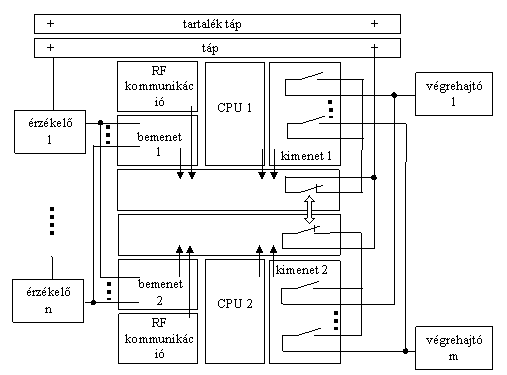
A redundancia növelése jelentősen növeli a költségeket. Az 1002D struktúra költséghatékony. Az 1002D struktúra hardver felépítése:
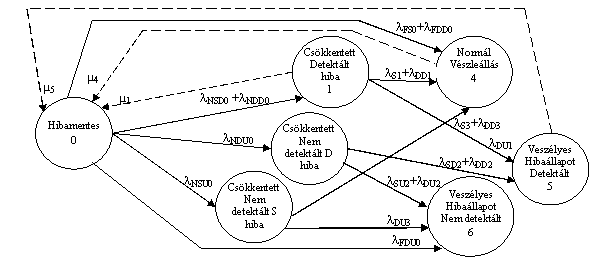
2. ábra Az 1002D struktúra. Ebben a struktúrában két processzordolgozik párhuzamosan. Mindkét processzornak saját be-, kimeneti, és kommunikációs kártyája van. Az érzékelők és a végrehajtók nincsenek duplikálva. Az azonos funkciót megvalósító be, és kimenetek párhuzamosan van kötve. A redundáns ágakat egy-egy diagnosztikai kártya felügyeli. A diagnosztikai kártya sorba köt egy kontaktust a kimeneti kártyával. Hibátlan működés esetén, a diagnosztikai kontaktusok zárt állapotban vannak. Kezelhető hiba esetén a hibás ág diagnosztikai kontaktusát nyitja, a működő ág kontaktusa zárva marad. Így a rendszer, mint 2002 struktúra viselkedik. Veszélyes hiba detektálása esetén bontja a diagnosztikai kontaktusokat, ami 1002 struktúrának megfelelő. A diagnosztikai kártyák között információs kapcsolat van, és mindkét kártya képes az azonos funkciójú kimeneti kártyák diagnosztikai kontaktusát kezelni. A közös távadók és végrehajtók miatt a tápellátást is közös. A megbízhatóság növelése érdekében célszerű redundáns tápellátást alkalmazni, és ezáltal formálisan a λA, és a λB valószínűség értékek meghatározásához az irányító rendszert két független (CPU, be-, és kimeneti I/O, kommunikáció, táp) 1001 struktúraként lehet elemezni. A szimmetrikus elrendezés következtében a λA, és a λB értékek azonosak. A diagnosztikai kártyák önálló elektronikák, melyeknek hibaarányát (λDA, λDB) szintén figyelembe kell venni. Ennek megfelelően a 3. táblázat az 1002D struktúra hibagyakoriságát definiálja. Látható, hogy az 1002D struktúra egyesíti az 1002 és a 2002 struktúrák előnyeit. A teljes rendszer kezdeti hibaaránya a <3.> kifejezéssel határozható meg λ0=λS+λD=λDA*λDB+λA*λB+(λDA+λDB )*(λA +λB) <3.> A λA, és λB a érték az eszköz, vagy technológia hibaelemzésével határozható meg. A sorba kötött eszközök hibavalószínűsége az eszközök hiba valószínűségének uniója, a párhuzamosan kötött eszközök hibavalószínűsége az eszközök hiba valószínűségének metszete. A szabványban [2] definiált módon, felépíthető a megbízhatósági blokk diagram. hibaelemzésben figyelembe kell venni, hogy a 3. ábra szerinti elrendezésben közösek az érzékelők, és a végrehajtók mindkét ág számára. A Markov modell A Markov modellben egy eszköz, vagy alrendszer, illetve a teljes rendszer működése egymást követő állapotok sorozatából áll, amelyek között az átmenetet valószínűségi változó írja le. Megbízhatóság vizsgálat csak néhány diszkrét állapotot (hibátlan, rejtett hibával, detektált hibával működés, illetve biztonságos vészleállás, baleset, stb.) tételez fel. Az átmenetek között valószínűségi változó teremt kapcsolatot. A veszélyesebb állapotba kerülés valószínűségét, más szavakkal a hibagyakoriságot, λ betűvel, a kevésbé veszélyesebb állapotba kerülés valószínűségét, más szavakkal a javíthatóságot µ betűvel szokás jelölni. A 3. ábrán látható, hogy az 1002D struktúra 7 állapottal írható le. Hibamentes állapotból (0) kerülhet hibás (4, 5, 6), és csökkentett biztonságú állapotokba (1, 2, 3). Hibamentes állapotból hibás állapotokba kerülésnek λF0 a valószínűsége. Csökkentett biztonságú állapotokban az egyik és csak az egyik redundáns ág hibásodik meg. Ilyenkor 1001D struktúrájú rendszerként az eszköz még üzemképes. Az egyik, vagy a másik ág meghibásodásának együttes valószínűsége λN0. A λ0 értékét, a következmények miatt, célszerű megosztani kezelhető, detektált (λSD0), veszélyes, detektált (λDD0), kezelhető, nem detektált (λSU0), és veszélyes, nem detektált (λDU0) hibaarányra. A normál üzem ("0" állapot) kezdeti valószínűsége 1-λ0. A λ0 bontható fel a 3. ábrán látható gráf "0" állapotból kifutó élek értékekre. A <3.> kifejezéssel meghatározott λ0 érték felbontásához ismerni kell a vezérlő berendezés részeinek, az érzékelőktől a végrehajtókig, SIL besorolását. Az egyes hibák kockázatának elemzésével bontható a λ0 a <4.> kifejezésben megadott részekre. λ0 = λN0+ λF0=λNSD0+λNSU0+λNDD0+λNDU0+λFS0+λFDD0 +λFDU0 <4.> Folytonos technológiák esetén, ha az eszköz vagy technológia detektált hibás állapotba kerül, akkor a hiba elhárítása után ismét a "0" állapotba jut vissza. A hibaelhárítás természeténél fogva diszkrét idejű folyamat, és a µi annak valószínűsége, hogy adott időtartamon belül megtörténik a hiba elhárítása.
3. ábra Általános 1002D Markov modell Az 1002D rendszerben a mátrix 7x7-es, mert a rendszert 7 állapot írja le. A 3. ábra alapján definiálható a
A működtetés folyamata mintavételezetten is vizsgálható. Így a folytonos jel helyett használhatjuk az időben diszkrét jelet. P(t) ? P(kT0) = P(k) <6.> Időben diszkrét jelekkel dolgozva kezelhető az ugrásszerű változás a jelben. Ez áthidalja azt a problémát, hogy az időszakosan működő eszközök vagy technológiák meghibásodás valószínűsége az energiamentesen tárolt, az időszakos teszt, és a folytonos üzemmódban eltérően változik. Az energiamentesen tárolt állapotban a meghibásodás valószínűsége az 1. ábra szerinti, de a meghibásodás rejtve marad. A teszt üzemmódban a végrehajtott műveletek típusa, és száma korlátozott, azonban az időszakos teszt üzemmód közben történhet meghibásodás, ami lényegében időkorlát nélkül javítható. A folytonos üzemmódban az IEC61511 szabványban [4] definiált módon számítható a meghibásodás valószínűsége. Ha az üzemben tartási idő 20 év ? 7300 [nap], akkor T0 = 3 [nap] mintavételezési idő elegendően sűrű, ezáltal a mintavételezett jel kvázi folytonosnak tekinthető, és így a folytonos rendszerekre kidolgozott eljárások alkalmazhatók. Azt, hogy a 3. ábra 7 állapotából az eszköz vagy technológia melyikben milyen valószínűséggel tartózkodik az
A Az energiamentesen tárolt üzemmódban a hibaarány változása A meghibásodás valószínűsége (1. kifejezés), és így az egyes állapotokban tartózkodás valószínűsége az üzemelési idő alatt folyamatosan változik. Végrehajtva a 7. kifejezésben megadott műveletet az
Energia mentes (tárolt) állapotokban a javítások valószínűségi változóihoz (µ1, µ4, µ5) tartozó a gráf élek nincsenek. Így a λi (i=1, 2, ..5) értékek kiszámítása is ennek megfelelő. Az időszakos teszt hatása a hibaarányra Az időszakos tesztek célja, hogy a hibaarány növekedését korlátozza. Folytonos technológiák esetén a detektált hibájú, csökkentett (1) állapotnak, és a hozzá tartozó µ1 értékének van kiemelt szerepe. A µ1 annak valószínűsége, hogy a folyamatos üzem nem szakad meg. A kezelő által észlelt hibás üzemállapotok (4, 5) a folytonos üzemmód megszakításával járnak, ami jelentős költség. Valószínűségi változóval (µ4, µ5) írják le, hogy az eszköz javítása adott időkorlát esetén megtörténik-e. A µ1, µ4, µ5 gráf élek csak az időszakos teszt idején aktívak. Az ilyenkor észlelt hibás üzemállapotok (1, 4, 5) kijavításának nincs időkorlátja. A vizsgálat szempontjából nem jelent erős kikötést, ha feltesszük, hogy az időszakos teszt, és az esetleges javítás egy mintavételnyi idő alatt (3 nap) biztosan befejeződik. A szerző javaslata, hogy a javítások valószínűségi változói (µ1, µ4, µ5) legyenek olyan értékűek, amellyel P(k+i) valószínűségi mátrix p11-es eleme, ami a normál üzem ("0" állapot) R(k+i) megbízhatósága, növekszik a javítás hatására. Az alábbi peremfeltételek fennállását természetesnek tekinthetjük: • Annak valószínűsége, hogy az i-edik mintavételi időpontban végzett teszt alatt a rendszer az 1-es, vagy 4-es, vagy 5-ös állapotba kerül rendre S1(k+i), S4(k+i), S5(k+i). • A javítás hatására a javított állapot a kezdeti (k=0, i=0) értékére áll vissza. • A javítások valószínűségi változói (µ1, µ4, µ5)) azonos µ0 értékűek.
Értelemszerűen az i-edik mintavételi időpontban végzett teszt alatt csak egy konkrét állapotba kerülhet az eszköz. A hibák, nem törvényszerűen, de lehetnek függetlenek, ezért az egyik hibás állapot javítása nem csökkenti a másik hibaállapotba kerülés valószínűségét. Nem megjósolható, hogy melyik állapot következik be. A szerző javaslata, hogy az S1, S4, S5 állapotok között a valószínűségűkkel súlyozottan legyen szétosztva a µ0 valószínűségi érték. Feltételezve, hogy a 7. kifejezéssel az
A folyamatos üzemmódban a hibaarány változása. A folyamatos üzemmódhoz [4] magas működés igényű (SIL) értékek tartoznak, λ [1/óra] dimenziójú. Elterjedt az 1 [év] ? 104 [óra] közelítés. Az Feltételezve, hogy egy - két mintavételnyi idő alatt ˙(T0 = 3 nap) a valószínűség értékek lineárisan változnak, c0 helyett használhatjuk a cT0 = 7,2*10-3 konstans értéket, és így a <7.> kifejezést végrehajtva 72 órához (T0=3 nap) tartozó változást kapunk. Valóságos bevetéskor a harctéri felderítő eszközök, a mobilrobotok, a légvédelmi rakéták ráemelő és kilövő eszközeinek javítására nincs mód, vagy idő, ezért a
együttes értéke adja meg. A vizsgálat menete A A Az energiamentesen tárolt, az időszakos teszt, és a folytonos üzemmódokra kidolgozott kifejezések felhasználásával vizsgálható: • Az időszakos tesz gyakoriságának hatása a megbízhatóságra. • Az λN0, λF0 arányának hatását a megbízhatóságra.
Irodalomjegyzék 1. IEC 61508. Functional safety of Electrical/Electronic/Programmable electronic Safety-R elated Systems, 1998 2. Neszveda, József. Redundáns struktúrák és a biztonság sérthetetlenség szint kapcsolata ZMNE, Hadmérnök, 2007 II. évf. 1. szám 3. Zsigmond, Gyula. Folytonos rendszerek megbízhatósági vizsgálata. Automatizálás, 1985 5.szám 4. IEC 61511-1, Functional safety - Safety integrated systems for the process industry sector - Part1: Framework, definitions, system, hardware and software requirements, 2002 5. Goble, William M., Cheddy, Harry. Safety Instrumented systems Verification |
© ZMNE BJKMK 2008.





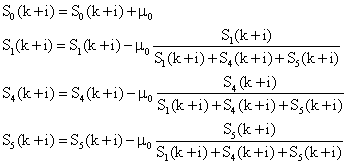 <10.>
<10.>